A Ruby programozási nyelv

Tanácsadó rendszer készítése a lineáris algebra könyvtárral és szinguláris felbontással

Tanácsadó rendszer készítése a lineáris algebra könyvtárral és szinguláris felbontással

Bevezetés

Tegyük fel, hogy van egy weboldalunk, ahol a felhasználók különböző termékeket értékelhetnek (például tévésorozatokat vagy könyveket) egy 1 és 5 közötti skálán. Szeretnénk tanácsot adni a felhasználóknak arról, hogy milyen sorozatot érdemes megnéznie, az alapján hogy más sorozatok mennyire tetszettek neki. Az amazon és a netflix oldalakon működik hasonló rendszer. Az amazon és netflix oldalakon van hasonló rendszer. A szinguláris érték felbontás az egyik legegyszerűbb és leghatékonyabb módszer erre a feladatra. Ruby-ban a linalg könyvtár mátrix műveleteit tudjuk egy ilyen tanácsadó rendszer implementálására használni.

Lineáris algebra könyvtár telepítése

Ha Linuxot használunk, akkor a linalg könyvátrhoz először fel kell telepítenünk a 'f2c' csomagot. A 'linalg' könyvtárnak még a 'lapack' ruby könyvtár is a függősége. Ezeket gem-en keresztül tudjuk a legegyszerűbben telepíteni:

gem install lapack
gem install linalg

A Lineáris algebra könyvtár

A linalg könyvtár lineáris algebrához kapcsolódó adatszerkezetek és lineáris algebrai műveletek (mátrixműveletek, felbontások) implementációit tartalmazza. Mivel túlságosan hosszú lenne a teljes lineáris algebra könyvtárról leírást készíteni (nagyon széles funkcionalitása miatt), ezért itt csak egy összefoglalót adok a legfontosabb függvényekről és módszerekről amik kellenek a tanácsadó rendszerhez. Teljes referenciát itt lehet találni a könyvtárról.

DMatrix osztály

Konstruktor

Háromféleképpen lehet új mátrixot létrehozni: 

DMatrix.new(vsize, hsize)
DMatrix.new(vsize, hsize, scalar)
DMatrix.new(vsize, hsize) { |i, j| ... }

Az első paraméterezés egy vsize sorból és hsize oszlopból álló mátrixot hoz létre 0-kkal feltöltve. Ha a scalar paraméter is meg van adva, akkor ezzel az értékkel tölti fel a mátrixot. Ha pontosabban meg akarjuk adni, hogy hogyan legyen feltöltve a mátrix, akkor átadhatunk egy blokkot is.

Példa: létrehozunk egy 4x4-es mátrixot, ahol az alsó háromszögben 1-esek, az átló felett 0-k vannak. 

DMatrix.new(4, 4) { |i, j| i > j ? 1 : 0 }
join_columns(cols)
A megadott oszlopvektorokból egy új mátrixot hoz létre.
join_rows(cols)
A megadott sorvektorokból egy új mátrixot hoz létre.
singular_value_decomposition => [u, s, vt]

Felbontja az M mátrixot úgy, hogy M = u * s * vt teljesül. Ha M m sorból és n oszlopból áll, akkor u,vt ortogonális mátrixok, s diagonális mátrix, és az átlóban az M szinguláris értékei vannak.

column(j)
Visszaadja a DMatrix j. oszlopát.
to_a
Egy DMatrix objektumnak visszaadja a kétdimenziós tömb reprezentációját.
columns(array)
Létrehoz egy új mátrixot az array-ban lévő oszlopvektorokból. Az array-ban lévő oszlopvektorok tömbként vannak megadva.
transpose
Visszaadja a mátrix transzponáltját.
norm
Visszaadja a mátrix 2-es normáját.

Egyéb lehetőségek

Mátrix műveletek:

Felbontások:

A műveletek teljes listája a könyvtár oldalán található.

Lineáris algebra alapok

A szinguláris érték felbontás egy mátrix felbontási módszer ahol egy mxn-es mátrixot három részre bontunk (M = USV*):

A szinguláris felbontás legnagyobb előnye, hogy segítségével olyan reprezentációt tudunk előállítani, ami kevesebb dimenzióban ábrázolja az adatainkat, de mégis jól közelíti az eredeti mátrixot. Egy nagy adathalmazt kevesebb biten tudunk tárolni. Az U és a V mátrix az eredeti mátrix két jellemzőjét (sorozatok és felhasználók) írja le m és n dimenzióban. Ha elhagyjuk az U,S,V mátrixok első n oszlopán kívül a többi oszlopot (az új mátrixokat jelöljük U',S',V' -vel), akkor egy olyan közelítést kapunk, ahol U',V' a sorozatoknak és felhasználóknak egy n dimenziós közelítése. Ha később egy új felhasználó kerül a rendszerbe, akkor könnyen tudjuk ennek a felhasználónak a vektorát vetíteni az n dimenziós térre, és nem kell az egész mx(n+1)-es mátrix felbontását és vetítését újra elvégezni.

Adatok eltárolása

Az oldalunkon lévő felhasználók értékeléseit egy mátrixban tároljuk, ahol minden sor egy sorozatnak felel meg, és minden oszlop egy felhasználó. A 0-ás érték azt jelenti, hogy a felhasználó még nem értékelte a sorozatot. A felbontásból kapott mátrixokat fel tudjuk használni az eredeti mátrix közelítésére.

Csaba Zoltán Béla Anna
Trónok harca 5 5 0 5
Breaking bad 5 0 3 4
Family guy 3 4 0 3
Dexter 0 0 5 3
Big Bang theory 5 4 4 5
NCIS 5 4 5 5

Hozzuk létre a mátrixot ami eltárolja az adatokat: 

users = { 1 => "Csaba", 2 => "Zoltan", 3 => "Bela", 4 => "Anna" }
m = Linalg::DMatrix[
            [5,5,0,5], # Trónok harca
            [5,0,3,4], # Breaking bad
            [3,4,0,3], # Family guy
            [0,0,5,3], # Dexter
            [5,4,4,5], # Big Bang theory
            [5,4,5,5]  # NCIS
            ]

Felbontás

Végezzük el a felbontást: 

u, s, vt = m.singular_value_decomposition
vt = vt.transpose

Hagyjuk el az első két oszlopon kívül a többit: 

u_p = Linalg::DMatrix.join_columns [u.column(0), u.column(1)]
v_p = Linalg::DMatrix.join_columns [vt.column(0), vt.column(1)]

Később szükségünk lesz az S' mátrix sajátértékeire, ezt számoljuk ki: 

eigenv = Linalg::DMatrix.columns [s.column(0).to_a.flatten[0,2], s.column(1).to_a.flatten[0,2]]

A következő mátrixokat kapjuk:

U'
-0.4472 0.5373
-0.3586 -0.2461
-0.2925 0.4033
-0.2078 -0.6700
-0.5099 -0.0597
-0.5316 -0.1887
S'
17.7139 0.0000
0.0000 6.3917
V'
-0.5710 0.2228
-0.4275 0.5172
-0.3846 -0.8246
-0.5859 -0.0532












Ez alapján ábrázolni tudjuk, hogy melyik felhasználó hasonló egymáshoz (a V' mátrix írja le a felhasználókat):
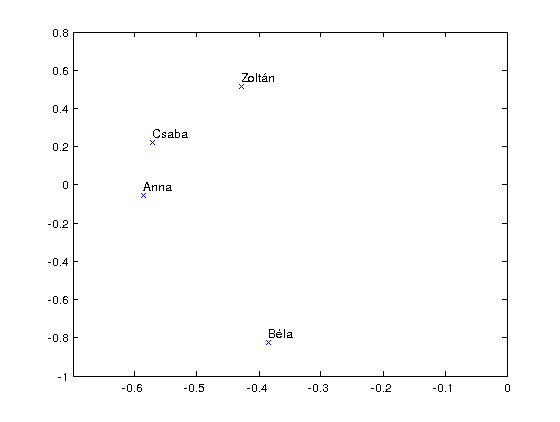
A felhasználók vetkorainak kétdimenziós projekciója
Látható, hogy a Csaba és Anna felhasználók nagyon közel vannak egymáshoz. Ez azt jelenti, hogy nagyon hasonló sorozatokat kedvelnek. Ezt fel tudjuk használni az ajánlórendszerhez. Meg kell keresnünk az adott felhasználóhoz leginkább hasonló felhasználót és azokat a sorozatokat ajánlani neki, amiket a másik a legmagasabbra értékelt.

Hasonló felhasználók keresése

Adjunk hozzá a rendszerhez egy új felhasználót, akinek a következő értékelései vannak: 5,5,0,0,0,5 (emlékeztető: minden szám egy sorozatnak felel meg). Ki tudjuk számolni az új felhasználó projekcióját az új térre:

x = [5,5,0,0,0,5]
x' = U' * S'^-1

Kódban: 

peter = Linalg::DMatrix[[5,5,0,0,0,5]]
peter_proj = peter * u_p * eigenv.inverse

Használjuk a koszinusz hasonlósági mértéket az új felhasználó (Péter) és az összes többi felhasználó közötti hasonlóság kiszámítására, aztán rendezzük csökkenő sorrendbe a hasonlóságokat. 

user_sim, users_num = {}, 1
v_p.rows.each { |x|
    user_sim[users_num] = (peter_proj.transpose.dot(x.transpose)) / (x.norm * peter_proj.norm)
    users_num += 1
  }
user_sim = user_sim.sort{ |x, y| y <=> x }

Legjobb sorozat keresése

Válasszuk ki a leginkább hasonló felhasználót 

other_user = m.column(user_sim[0][0]-1).transpose.to_a.flatten
peter = peter.transpose.to_a.flatten

Olyan sorozatot szeretnénk ajánlani, amit Péter még nem látott. Válasszuk ki ezeket az elemeket: 

new_series = {}
peter.each_index { |i|
  new_series[i+1] = other_user[i] if peter[i] == 0 and other_user[i] != 0
}

Rendezzük a még nem látott sorozatok értékeléseit, és adjuk vissza a legjobbra értékeltet: 

new_series = new_series.sort{|a,b| b <=> a}

series = [
            "Trónok harca",
            "Breaking bad",
            "Family guy",
            "Dexter",
            "Big Bang theory",
            "NCIS"
]

printf "Ajánlott sorozat: %w\n", series[new_series[0][0]]