1. Kvázipárhuzamosság a Simulában (QPS)
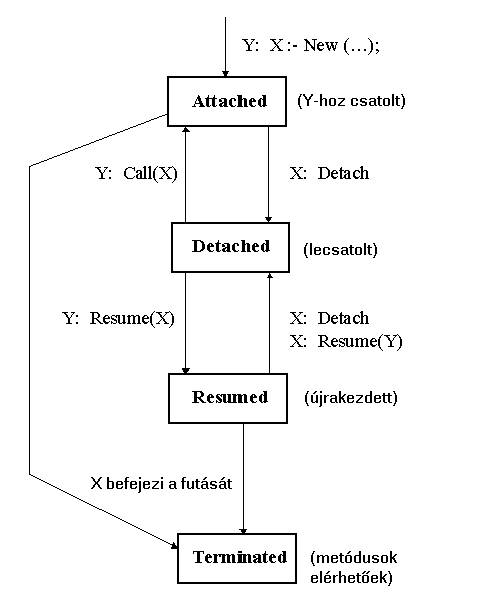
Az objektumok életvonalát a Simula olyan korutinokkal (kooperatív rutin) modellezi, melyek képesek egyes belépési pontjaikon átmenetileg megállni, majd folytatni működésüket. A (kvázi)párhuzamosságnak két szintje van. Az első szinten nem jelenik meg az idő, csupán a programozó gondolkodik "kvázi” párhuzamosan, a második szint vezeti be az idő fogalmát, ahol a programozó (felhasználói szemszögből) párhuzamos folyamatokkal dolgozik. Az első szinthez bármilyen osztályt felhasználhatunk, azonban a második szinthez a Simulation rendszerosztály Process osztályára kell építenünk. A lenti ábra szemlélteti egy X objektum korutinjának (törzsének) lehetséges állapotait. Ha egy törzs nem veszi fel a köztes állapotok egyikét sem, akkor először csatolt (attached), majd terminált (terminated) állapotú lesz. (Más objektum-orientált nyelvek objektumai mindig terminálnak). Egy terminált objektum a továbbiakban is használható marad, így el lehet érni a műveleteit és/vagy az attribútumait.
A Simula az alábbi lehetőségekkel (azaz minden osztályban elérhető metódusokkal) támogatja a kvázi párhuzamos rendszerekkel (QPS, QuasiParallel System) való munkát:
Detach: megállítja az aktuális objektum futását (az aktuális objektum az, amelyikre meghívtuk a Detach-et). Az aktuális objektum leválasztott (detached) állapotba kerül. A vezérlés átadódik arra a pontra, ahol az aktuális objektum létrejött vagy átvette a vezérlést.
Resume(Y): aktiválja a leválasztott (detached) Y objektumot, ami így éber (resumed), az aktuális objektum (az, ahonnan a metódust meghívtuk) pedig leválasztott (detached) állapotba kerül.
Call(Y): hasonlít a Resume-ra, de az Y objektum az aktuális objektumhoz lesz csatolva (attached). Az aktuális objektum ezzel leválasztott (detached) állapotba kerül, majd futása akkor folytatódik, amint az Y kerül leválasztott (detach) állapotba.
QPS 1. példa: Sakk játszma vezérlése „Két mester” megközelítéssel
A következő programban három korutin szerepel: a két játékos és a főblokk. Meg kell jegyeznünk, hogy az első két lépés különleges kezdőlépés. Egy játékos csak a harmadik lépéstől kezdve nyerheti meg bizonyos valószínűséggel a játszmát: a Draw(0.3, Seed) egy logikai függvény, mely 0,3-es valószínűséggel ad vissza igaz értéket. Figyeljük meg, ahogy a főblokk létrehozza a két játékost, összeköti őket az ellenfél (Opponent) attribútumaikon keresztül és a Resume művelettel átadja a vezérlést a fehérnek. Ezután a játékosok felváltva lépnek, ami addig folytatódik amíg az egyikük meg nem nyeri a játszmát. Ez terminálja korutinjaikat és a vezérlés átadódik a főblokknak.
Begin
Boolean Mate;
Ref(Player) White, Black, Winner;
Integer Seed;
Class Player(PName); Text PName;
Begin
Ref(Player) Opponent;
Integer Move;
! The life follows;
Detach;
OutText(PName); OutText("'s First Move"); OutImage;
Resume(Opponent);
OutText(PName); OutText("'s Second Move"); OutImage;
Resume(Opponent);
Move := 2;
While not Mate do begin
Move := Move+1;
OutText(PName); OutText("'s Move # ");
OutInt(Move,3); OutImage;
If Draw(0.3,Seed) then begin
Mate := true; Winner :- This Player;
End If;
Resume(Opponent);
End While;
End of Player;
Begin ! QPS head;
OutText("Creating Players, Starting the white one"); OutImage;
White :- New Player("White");
Black :- New Player("Black");
White.Opponent :- Black;
Black.Opponent :- White;
Seed := 17;
Resume(White);
OutText("Finish: "); OutText(Winner.PName);
OutText(" won in move"); OutInt(Winner.Move,3); OutImage;
End of QPS
End of program;
Ez a formázott kimenete a fenti programnak. A behúzás mutatja az objektumot, mely generálja a kimenetet (balról-jobbra rendre): főblokk, fehér (White), fekete (Black).
Creating Players, Starting the white one
White's First Move
Black's First Move
White's Second Move
Black's Second Move
White's Move # 3
Black's Move # 3
White's Move # 4
Black's Move # 4
Finish: Black won in move 4QPS 2. példa: Sakk játszma vezérlése „Mester és két szolgája” megközelítéssel
A következő programban három korutin szerepel: a két játékos és a főblokk. A különbséget ez és az előző program között a főprogram aktívabb szerepe jelenti. Itt nem a játékosok adják át egymásnak a vezérlést, hanem csak lépnek majd leválasztott állapotba kerülnek. A főprogram ismétlődően aktiválgatja őket, míg az egyikük meg nem nyeri a játékot. Figyeljük meg, hogy a Call parancs használatával a játékosok újra és újra a főblokkhoz csatolják magukat.
Begin
Boolean Mate;
Ref(Player) White,Black,Winner;
Integer Seed;
Class Player(PName); Text PName;
Begin
Ref(Player) Opponent;
Integer Move;
! The life follows;
Detach;
OutText(PName); OutText("'s First Move"); OutImage;
Detach;
OutText(PName); OutText("'s Second Move"); OutImage;
Detach;
Move := 2;
While true do begin
Move := Move+1;
OutText(PName); OutText("'s Move # ");
OutInt(Move,3); OutImage;
If Draw(0.05,Seed) then begin
Mate := true; Winner :- This Player;
end;
Detach;
End While;
End Player;
Begin
OutText("Creating Players, Starting the game"); OutImage;
White :- New Player("White");
Black :- New Player("Black");
White.Opponent :- Black;
Black.Opponent :- White;
Seed := 11;
While not Mate do begin
Call(White);
If not Mate then Call(Black)
End While;
OutText("Finish: "); OutText(Winner.PName);
OutText(" won in move"); OutInt(Winner.Move,3); OutImage;
End
End;
Ez a formázott kimenete a fenti programnak. A behúzás mutatja az objektumot, mely generálja a kimenetet (balról-jobbra rendre): főblokk, fehér (White), fekete (Black).
Creating Players, Starting the game
White's First Move
Black's First Move
White's Second Move
Black's Second Move
White's Move # 3
Black's Move # 3
White's Move # 4
Black's Move # 4
White's Move # 5
Black's Move # 5
White's Move # 6
Finish: White won in move 6QPS 3. példa: Sakk játszma vezérlése „Mester és két szolgája” megközelítéssel, csomagként implementálva
A következő programban a fő osztály (Chess) két lokális osztályt deklarál: a Player-t és a Referee-t. A szimulációt a főprogram készíti elő a játékra, életvonala elején létrehozza és összekapcsolja a két játékost és a játékvezetőt. Mind a három objektum lecsatlakozik (detached lesz) és a fő osztály is terminál. A játékot az alább leírt programmal kell elindítani (amelyik prefixként használja a Chess-t). A prefixként való használat importál minden deklarációt és előkészíti a játékot. Vegyük észre, hogy a program csupán aktiválja a játékvezetőt és kiértékeli a játékot, de nem vezérli.
Class Chess; ! Main class with local: Player, Referee;
Begin
Boolean Mate;
Ref(Player) White,Black,Winner;
Ref(Referee) Master;
Integer Seed;
Class Player(PName); Text PName;
Begin
Ref(Player) Opponent;
Integer Move;
! The life of Player;
Detach;
OutText(PName); OutText("'s First Move"); OutImage;
Detach;
OutText(PName); OutText("'s Second Move"); OutImage;
Detach;
Move := 2;
While true do begin
Move := Move+1;
OutText(PName); OutText("'s Move # ");
OutInt(Move,3); OutImage;
If Draw(0.05,Seed) then begin
Mate := true; Winner :- This Player;
end;
Detach;
End While;
End Player;
Class Referee;
Begin
Detach;
While not Mate do begin
Call(White);
If not Mate then Call(Black)
End While
End of Referee;
Begin ! Life of Chess;
Seed := 11;
OutText("Creating the Players and the Master"); OutImage;
White :- New Player("White");
Black :- New Player("Black");
White.Opponent :- Black;
Black.Opponent :- White;
Master :- New Referee;
End
End of Chess;
A következő programrészlet a fő osztályt prefixként használja:
External Class Chess;
Chess Begin
OutText("Resuming the Master"); OutImage;
Resume(Master);
OutText("Finish: "); OutText(Winner.PName);
OutText(" won in move"); OutInt(Winner.Move,3); OutImage;
End of Program;
Ez a formázott kimenete a fenti programnak. A behúzás mutatja az objektumot, mely generálja a kimenetet (balról-jobbra rendre): főblokk, fehér (White), fekete (Black).
Creating the Players and the Master
Resuming the Master
White's First Move
Black's First Move
White's Second Move
Black's Second Move
White's Move # 3
Black's Move # 3
White's Move # 4
Black's Move # 4
White's Move # 5
Black's Move # 5
White's Move # 6
Finish: White won in move 62. Szimuláció avagy a párhuzamos folyamatok világa
A Simulation rendszerosztály alapfogalma a Process – mely szekvenciális események (kódszegmensek által reprezentált) sorozata, melyeket passzív periódusok választanak el egymástól. A lenti ábra mutatja Simulation-ben deklarált osztályokat és azok metódusait. Az Event Notice (a Link leszármazottja) egy tervezett eseményt reprezentál, ami egy meghatározott időpontban (EvTime) hajtódik majd végre. A Proc az a folyamat, aminek a kódszegmense aktiválódni fog. Az SQS (a Head leszármazottja) pedig egy lista, melyben az események időrend szerint helyezkednek el. Ez a diszkrét szimulációs nyelvek úgynevezett naptárának felel meg. Koncepcionálisan ez egy rendezett láncolt lista, azonban belül általában egy jóval hatékonyabb bináris fa adatszerkezettel kerül megvalósításra. Természetesen ez a lista nem érhető el közvetlenül a felhasználói programból. Léteznek olyan, később tárgyalt ütemezők, melyek támogatják az idő figyelembe vételét és a folyamatok kölcsönös szinkronizációját. A felhasználói program folyamatai leszármazottai a közös ős Process osztálynak. Az első két metódus az állapotot teszteli, míg a másik kettő visszaadja a következő beütemezett eseményt és az aktiválási időt.
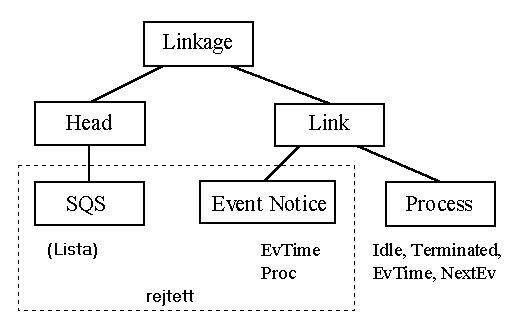
A Simulation rendszer szolgáltatásai az „alacsonyszintű” kváziparallel eljárásokkal (detach, resume, call) kerültek implementálásra, csak felhasználóbarátabb módon. A Simulation használója ”párhuzamosan gondolkodik”. A szimulációs modell dinamikáját a kölcsönösen kapcsolatba lépő párhuzamos folyamatok fejezik ki. Ez egy teljesen természetes megközelítés – lévén pontosan így működik a valós világ is.
Process objektumok állapotai:- Aktív (active): a folyamat egy szegmense végrehajtás alatt áll.
- Felfüggesztett (suspended): a folyamat be van jegyezve az SQS-be. Amennyiben nem törlik, a folyamat aktiválásra fog kerülni.
- Passzív (passive): nincs beütemezett eseménye. Egy másik folyamatnak kell majd aktiválnia.
- Terminált (terminated): a folyamat befejeződött. Nem aktiválható újra.
Időzítési, sorbaállítási és szinkronizációs lehetőségek:
- Activate X: aktivál egy X passzív folyamatot.
- Reactivate X: vagy aktivál egy passzív folyamatot, vagy megváltoztatja a következő aktiváció idejét ha a folyamat felfüggesztett vagy aktív.
- Hold(T): T késedelmet generál a folyamat életében.
- Passivate: az aktuális folyamatot passzívvá teszi.
- Cancel(X): törli X következő aktiválását.
- Wait(Q): Hasonló mint a Passivate, de egyúttal a Q sor végére is helyezi a folyamatot.
1. Példa: Többcsatornás sorba rendező rendszer, „Aktív ügyfél, passzív pénztáros” megközelítéssel
Az alábbi ábra a rendszer szimulációját mutatja. Ez egy bank absztrakciója, aholis az ügyfelek a pénztároshoz vezető sorokban várakoznak. A bankba belépő ügyfelek vételtelen, 1 és 3 perc között egyenletesen elosztott időközönként érkeznek. Minden pénztárosnak azonos, véletlenszerű kiszolgálási ideje van, normál eloszlással, 8 perc várható értékkel és 2 perc szórással. A szimuláció feladata hogy meghatározza az egy ügyfél által átlagosan a bankban eltöltött időt. A hasonló rendszerek szimulációja Simula-ban (pontosabban a Simula Simulation rendszer-osztályában) mindig a folyamat beazonosításával indul. Egy folyamat nyilván az ügyfelek előállítója lesz – ez ismétlődően generálja az ügyfeleket, rögzíti a beérkezési időket és véletlen ideig várakozik. A rendszer dinamikájának kifejezésére két logikai megközelítés létezik. Az egyik (amit ebben a példában használunk) alapja az aktív ügyfelek és a passzív pénztáros. A másik megközelítés – az aktív pénztáros és a passzív ügyfelek – a következő példában található meg.
Egy aktív ügyfél életvonalán a következő lépések követhetőek:- Ha a pénztáros szabad, haladjon tovább. Ellenkező esetben várjon tovább a sorban.
- Foglalja le a pénztárost egy generált véletlen ideig, ami a kiszolgálási időt reprezentálja.
- Távozzon a pénztártól.
- Ha van a sorban várakozó ügyfél (nem lehet üres a sor), vegye ki onnan és aktiválja. (Az aktivált ügyfél a 2. lépéstől kezdi meg tevékenységét.)
- Statisztika frissítése.
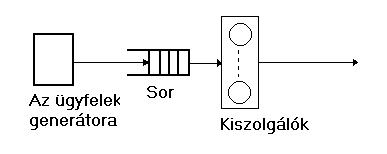
A következő szimulációs modell szimulálja a fenti rendszert. Az elsődleges cél az volt, hogy a modell logikáját egy, a lehető legegyszerűbb programon mutassuk be. Igazi szimulációs modellek természetesen több paraméterrel rendelkezhetnek és többféle eredményt is adhatnak (mint például az átlagos és maximális sorhossz, stb.) A következő programban két folyamat van jelen a kísérlet teljes időtartalma alatt: a generátor és a főprogram, ami addig vár amíg a kísérlet le nem fut, majd megjeleníti a végeredményt. Ezen kívül változó számban ügyfél folyamatok is léteznek ideiglenesen. A statisztika frissítése után terminálnak. Figyeljük meg, milyen szabványos könyvtári eljárásokat használunk a véletlen számok előállítására. A legtöbb, gyakran használt eloszláshoz létezik megvalósítás a Simula-ban. A véletlen generálás egy egész értékről kerül inicializálásra. Így arra is lehetőségünk van, hogy minden véletlen változót külön kezeljünk, de arra is, hogy egy-egy közös véletlen folyamon belül generáljunk értékeket.
! Active customer approach;
Simulation Begin
Real TrialDuration; ! Experiment length [min];
Ref(Head) Queue; ! The queue;
Integer Servers; ! Total number of servers;
Integer BusyServers; ! Numbers of working servers;
Integer TrialSeedG, TrialSeedS; ! Seeds of random generators;
Long Real TotalTime, TimeSpent; ! Variables for statistics;
Integer CustomersOut; ! Number of served customers;
Real MinInt, MaxInt; ! Uniform interval between arrivals;
Real SMean, SStd; ! Normal service duration;
Process Class Generator;
Begin
While true do begin
Activate New Customer(Time); ! Time is the current (arrival) time;
! Interval between arrivals: ;
Hold(Uniform(MinInt, MaxInt, TrialSeedG));
End While;
End of Generator;
Process Class Customer(Arrival); Real Arrival;
Begin
Ref(Customer) Next;
If not Queue.Empty or (BusyServers >= Servers) then
Wait(Queue); ! Customer has to wait in the Queue;
! Service can start: ;
BusyServers := BusyServers + 1; ! Seize a server;
! This is the teller service: ;
Hold(Normal(SMean, SStd, TrialSeedS));
BusyServers := BusyServers - 1; ! Release the server;
If not Queue.Empty then begin
Next :- Queue.First;
Next.Out; ! First from Queue served;
Activate Next after Current;
End If;
CustomersOut := CustomersOut + 1; ! Statistics;
TotalTime := TotalTime + (Time - Arrival);
End of Customer;
! MAIN program body: ;
TrialSeedG := 7; TrialSeedS := 23; ! Seeds for random variables;
MinInt := 1; MaxInt := 3; ! Min and Max intervals;
SMean := 8; SStd := 2; ! Random normal servers;
OutText("Enter the number of Servers : "); OutImage;
Servers := InInt; ! Initial numbers;
TrialDuration := 600; ! Other variables initialized to 0;
Queue :- New Head; ! Create an empty queue;
Activate New Generator; ! This starts the experiment;
Hold(TrialDuration); ! Experiment duration;
TimeSpent := TotalTime/CustomersOut;
OutText("Average time spent in the system: ");
OutFix(TimeSpent, 3, 10); OutImage;
InImage
End of program;
2. Példa: Többcsatornás sorba rendező rendszer, „Passzív ügyfél, aktív pénztáros” megközelítéssel
Ugyanúgy az előző példában leírt rendszert fogjuk szimulálni. A különbség az aktív szerver, ami ismétlődően szolgálja ki az ügyfeleket a sorból, amíg az ki nem ürül. Ezután a szerver passzív állapotba kerül. Az ügyfél feladata hogy aktiváljon egy üres szervert (ha van ilyen), majd álljon be annak sorába. Ez természetesen nem túl hatékony, de könnyen kezelhető. Az ügyfelek ezután a kiszolgálók által lesznek ismételten aktívak. Továbbiakban az ügyfelek már csak frissítik a statisztikát. A főprogram aktiválja az összes kiszolgálót, bár azonnal passzívak lesznek, mert a sorok üresek. Ezután a főprogram aktiválja a generátort majd vár, hogy befejeződjön a kísérlet.
! Active server approach;
Simulation Begin
Real TrialDuration; ! Experiment length [min];
Ref(Head) Queue; ! The queue;
Integer Servers; ! Total number of servers;
Integer TrialSeedG, TrialSeedS; ! Seeds of random generators;
Long Real TotalTime, TimeSpent; ! Variables for statistics;
Integer CustomersOut; ! Number of served customers;
Real MinInt, MaxInt; ! Uniform interval between arrivals;
Real SMean, SStd; ! Normal service duration;
Ref(Server) Array ServBank(1:10); ! Max. number of servers is 10;
Integer i;
Process Class Generator;
Begin
While true do begin
Activate New Customer(Time);
! Interval between arrivals: ;
Hold(Uniform(MinInt, MaxInt, TrialSeedG));
End While;
End of Generator;
Process Class Server;
Begin
Ref(Customer) ServedOne;
While true do
If not Queue.Empty then begin
ServedOne :- Queue.First;
ServedOne.Out; ! First from Queue served;
Hold(Normal(SMean, SStd, TrialSeedS));
Activate ServedOne after Current
end
Else
Passivate;
End of Server;
Process Class Customer(Arrival); Real Arrival;
Begin
For i:=1 step 1 until Servers do
If ServBank(i).Idle then
Activate ServBank(i) after Current;
Wait(Queue);
! Service finished: ;
CustomersOut := CustomersOut + 1; ! Statistics;
TotalTime := TotalTime + Time - Arrival;
End of Customer;
! MAIN program body: ;
TrialSeedG := 7; TrialSeedS := 23; ! Seeds for random variables;
MinInt := 1; MaxInt := 3; ! Min and Max intervals;
SMean := 8; SStd := 2; ! Random normal servers;
OutText("Enter the number of Servers : "); OutImage;
Servers := InInt; ! Initial numbers;
TrialDuration := 600;
Queue :- New Head;
For i:=1 step 1 until Servers do begin
ServBank(i) :- New Server;
Activate ServBank(i) ! Create and activate all servers;
End For;
Activate New Generator; ! This starts the experiment;
Hold(TrialDuration); ! Experiment duration;
TimeSpent := TotalTime / CustomersOut;
OutText("Average time spent in the system: ");
OutFix(TimeSpent, 3, 10); OutImage;
InImage
End of program;
3. A Simula beágyazott kvázi párhuzamos rendszerei
Egy kvázi párhuzamos rendszer (QPS) Simula-ban alapvetően egy blokk (általában, de nem feltétlenül egy prefixelt blokk), ami a törzsében létrehoz néhány objektumot, aztán a főblokkal együtt felépíti a rendszer kvázi párhuzamos korutinjait. Mivel a Simula (eltérően például a Pascaltól) egy igazi blokkszerkezetes nyelv, ezért blokk (ami általában egy QPS-t jelent) bárhol elő tud fordulni a kódban kifejezésként. Ez azt jelenti hogy egy QPS tartalmazhat további (beágyazott) QPS-eket, melyek szintén tartalmazhatnak további QPS-eket, stb. Ez az egyszerű szabály lehetőséget ad hogy hihetetlenül összetett szerkezeteket hozzunk létre. A következő program az egymásba ágyazás egy lehetséges használatát mutatja be egy sakkjátszma vezérlésén keresztül.
Beágyazott QPS példa: sakkjátszma vezérlése, a döntést támogató szimulációval
Képzeljük el, hogy egy sakk játékos szimulálja a játszmát, következő lépésének lehetséges következményeit illetően. A következő program (a „Két mester” megközelítésre alapozva) vázol egy lehetséges megoldást. A Player osztálynak van egy TestStrategy nevű metódusa, mely előkészíti a döntést. Ez egy, a külsőhöz hasonló QPS megoldást implementál. Tartalmaz egy lokális TestPlayer osztályt, amely nagyon hasonlít a külső Player osztályra, a TestStrategy metódus kivételével (ez lehet hasonló, de a beágyazást le kell állítani egy szint után). A TestStrategy törzse a belső QPS, melynek eredményeit felső szint a Player osztálya használja fel.
Begin
Boolean Mate;
Ref(Player) White, Black, Winner;
Integer Seed;
Class Player(PName); Text PName;
Begin
Ref(Player) Opponent;
Integer Move;
Procedure TestStrategy;
Begin
Class TestPlayer ... ;
Begin
! Internal experiment, similar to the outer QPS;
...
End of internal QPS;
End of TestStrategy;
! The life of Player;
Detach;
TestStrategy;
OutText(PName); OutText("'s First Move"); OutImage;
Resume(Opponent);
TestStrategy;
OutText(PName); OutText("'s Second Move"); OutImage;
Resume(Opponent);
Move := 2;
While not Mate do begin
Move := Move+1;
TestStrategy;
OutText(PName); OutText("'s Move # ");
OutInt(Move,3); OutImage;
If Draw(0.3,Seed) then begin
Mate := true;
Winner :- This Player;
End If;
Resume(Opponent);
End While;
End of Player;
Begin ! This block is the outer QPS head;
OutText("Creating Players, Starting the white one"); OutImage;
White :- New Player("White");
Black :- New Player("Black");
White.Opponent :- Black;
Black.Opponent :- White;
Seed := 17;
Resume(White);
OutText("Finish: "); OutText(Winner.PName);
OutText(" won in move"); OutInt(Winner.Move,3); OutImage;
End of outer QPS;
End of program;
4. A Simula beágyazott szimulációja
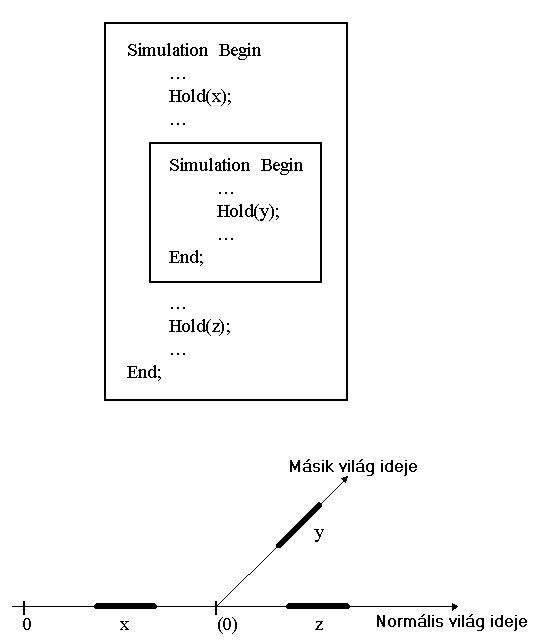
A kvázi párhuzamosságnak Simula-ban két szintje van, és mindkettőben lehet implementálni beágyazott rendszereket. Az előzőekben példát láthattunk az alacsony szintű beágyazásra. A Simulation rendszer-osztály bevezeti az idő fogalmát. Ez azt jelenti, hogy a beágyazás, megjelennek belső (beágyazott) idők is. Az alapötletet az alábbi ábra mutatja. A Hold metódus x és z idejei a külső időre vonatkoznak, az y idő viszont már egy másik világ belső idejére vonatkozik. Tehát Simula lehetőségünk van a sci-fik távoli jövőjében található rendszerek szimulálására is, de van ennek a lehetőségnek gyakorlati alkalmazása is. Így például lehetőségünk van olyan rendszereket szimulálnunk, ahol a szimuláció a döntéshozás részeként szerepel. Gondoljuk át a következő helyzetet: adott egy bonyolult rendszer és szakértők egy csoportja, akik különböző javaslatokkal állnak elő, amelyek következményeit nem lehetséges triviális vagy analitikus módon kipróbálni. (Véletlenül nem pont ez a leggyakoribb eset?) A döntési javaslatok tesztelése és kiértékelése érdekében a szakértők szimulációs megfigyeléseket végeznek, majd összehasonlítják az eredményeket és kiválasztják a legígéretesebb döntés(eke)t. Tegyük fel, hogy most ezt szimuláljuk.
Példa beágyazott szimulációra: Sorral rendelkező hálózat
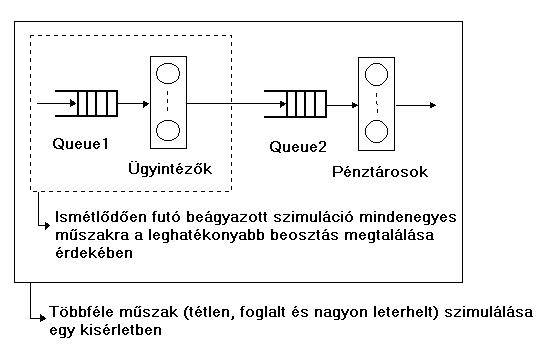
A lenti ábra mutatja a rendszer szimulációját. Ez egy bank absztrakciója, aholis az ügyfeleknek először ügyintézőkhöz vezető sorokban kell várakozniuk. Miután az ügyintéző kiszolgálta őket, az ügyfelek a pénztárosokhoz fáradnak, akikhez külön sor tartozik. A beérkezések közötti véletlen idő illetve az ügyintéző és a pénztáros véletlen hosszú kiszolgálási ideje ismert. Tegyük fel hogy van egy bizonyos számú munkatárs, akik képesek akár ügyintézőként, akár pénztárosként is dolgozni. A bank vezetősége le akarja tesztelni a munkatársak ügyintézővé illetve pénztárosa való beosztását a szokásos műszakokban: tétlen, foglalt és nagyon leterhelt, az ügyfelek beérkezése közti változó intervallumokkal.
A leghatékonyabb beosztás megtalálása érdekében a beágyazott szimuláció a következőképpen használható: minden periódus elején, a belső, ismétlődően futó szimuláció megvizsgálja az első szakasz eredményeit, az ügyintézők változó száma alapján (értelemszerűen ez a tartomány 1-től a lehető legtöbb munkatársig terjed). Ezen belső szimuláció eredményei alapján dönti el a vezetőség, hogy hány munkatárs dolgozzon ügyintézőként, és hány pénztárosként. A program leegyszerűsítése érdekében, ezt a döntést a felhasználó hozza meg, aki megkapja a belső szimuláció eredményeit, majd megkérjük, hogy adja meg az ügyintézők és pénztárosok számát. A döntést az első szakaszban eltöltött átlagos idő alapján kell meghozni, de érdekes lehet a leghosszabb rendszerben eltöltött idő is.
A következő „program” a szimuláció programjának vázlata (amit később részletezünk). Jegyezzük meg, hogy a belső blokk, amit a Simulation prefixel, minden lehetséges ügyintéző-pénztáros számra háromszor ismétlődően kerül lefuttatásra. A külső blokkéhoz hasonló osztályok deklarációit tartalmazza, a különbség az ügyfelek egyszerűbb viselkedésében mutatkozik meg, ugyanis itt csak egy kiszolgálási szakasz van. További beágyazás sincs. A szerkezet alapvetően nagyon hasonló az előző részben kifejtett „aktív ügyfél – passzív kiszolgáló” megközelítéshez.
Simulation Begin
Declaration of global variables
Process Class Generator; Begin ... End;
Process Class Customer; Begin ... End;
Initialize the global experiment
For Period:=1 step 1 until 3 do begin
For Trial:=1 step 1 until MaxClerks do
Simulation Begin
Declaration of internal global variables
Process Class Igenerator; Begin ... end;
Process Class Icustomer; Begin ... End;
Perform and evaluate one inner experiment
End of internal simulation;
Show results of internal experiments;
Select the best numbers of tellers and cashiers;
Perform a part of outer experiment for this period
End For;
Evaluate the global experiment
End of program;
A következő program a beágyazott szimuláció, a fenti szerkezettel.
! NESTED Simulation using the Simula's class SIMULATION ;
! ;
! The example is a model of a bank. Customers are first ;
! served by tellers, then by cashiers. ;
! The input rate changes in three periods: there is a busy ;
! period, then an idle period and again a busy one. ;
! For each period the repeated inner simulation experiment ;
! simulates the first queue for the particular input rate ;
! and for various numbers of servers. Then it shows the ;
! results (average time spent at the first server) and ;
! prompts the user for the number of tellers and the number;
! of cashiers. Tellers always finish a service that has ;
! already started. The simulation should find the ;
! time customers spend in the bank (average and maximum) ;
! for various numbers of clerks in the three periods. ;
! ;
Simulation Begin
! Global variables: ;
Integer Period,Trial; ! Period, Trial number;
Real Array MinInt,MaxInt(1:3); ! Min and Max intervals;
Real Array Duration(1:3); ! Duration of periods [min];
Ref(Head) Queue1,Queue2; ! The two queues;
Integer MaxClerks, Tellers, Cashiers; ! Total numbers;
Integer BusyTellers, BusyCashiers; ! Numbers of working clerks;
Real S1Mean, S1Std, S2Mean, S2Std; ! Random normal servers;
Integer SeedG, SeedS1, SeedS2; ! Seeds of the random generators;
Long Real TotalTime, MaxTime; ! Variables for statistics;
Integer CustomersOut; ! Number of served customers;
Process Class Generator;
Begin
While true do begin
! Interval between arrivals: ;
Hold(Uniform(MinInt(Period),MaxInt(Period),SeedG));
Activate New Customer(Time);
End While;
End of Generator;
Process Class Customer(Arrival); Real Arrival;
Begin
Ref(Customer) Next;
Real Spent;
If (not Queue1.Empty) or (BusyTellers >= Tellers) then
Wait(Queue1); ! Has to wait in Queue1;
! Service can start;
BusyTellers := BusyTellers + 1;
Hold(Normal(S1Mean, S1Std, SeedS1)); ! This is the teller service;
BusyTellers := BusyTellers - 1;
If (not Queue1.Empty) and (BusyTellers < Tellers) then begin
Next :- Queue1.First;
Next.Out; ! First from Queue1 served;
Activate Next after Current;
End If;
If (not Queue2.Empty) or (BusyCashiers >= Cashiers) then
Wait(Queue2); ! Has to wait in Queue2;
! Service can start;
BusyCashiers := BusyCashiers + 1;
Hold(Normal(S2Mean, S2Std, SeedS2)); ! This is the cashier service;
BusyCashiers := BusyCashiers - 1;
If (not Queue2.Empty) and (BusyCashiers < Cashiers) then begin
Next :- Queue2.First;
Next.Out; ! First from Queue2 served;
Activate Next after Current;
End If;
CustomersOut := CustomersOut + 1;
Spent := Time - Arrival;
TotalTime := TotalTime + Spent;
If Spent > MaxTime then MaxTime := Spent;
End of Customer;
Procedure Report; ! Experiment evaluation;
Begin
OutText(" *** Report on external simulation ***"); OutImage;
OutInt(CustomersOut,6); OutText(" customers ready at time ");
OutFix(Time,2,10); OutImage;
OutText("Average time in system: ");
OutFix(TotalTime/CustomersOut,2,10); OutImage;
OutText("Maximum time in system: ");
OutFix(MaxTime,2,10); OutImage;
End of Report;
! MAIN program body;
SeedG := 11; ! Seeds of random variables;
SeedS1 := 13;
SeedS2 := 17;
MinInt(1) := 1; MaxInt(1) := 4; ! Min and Max intervals;
MinInt(2) := 2; MaxInt(2) := 9;
MinInt(3) := 1; MaxInt(3) := 3;
Duration(1) := 120; ! Duration of periods;
Duration(2) := 240;
Duration(3) := 120;
MaxClerks := 6;
S1Mean := 6; ! Random normal servers;
S1Std := 1;
S2Mean := 8;
S2Std := 2;
Queue1 :- New Head;
Queue2 :- New Head;
Period := 1;
Activate New Generator;
For Period:=1 step 1 until 3 do begin
Real Array TimeSpent(1:MaxClerks);
OutText(" *** Results of internal simulation *** Period ");
OutInt(Period,1); OutImage;
OutText(" Tellers Average time spent"); OutImage;
For Trial:=1 step 1 until MaxClerks do
! ********************************************************** ;
Simulation Begin
! Internal Global variables: ;
Real TrialDuration; ! Internal experiment [min];
Ref(Head) Queue; ! The queue;
Integer Servers; ! Total number;
Integer BusyServers; ! Numbers of working clerks;
Integer TrialSeedG,TrialSeedS; ! Seeds of the random generators;
Long Real TotTime; ! Variables for statistics;
Integer CustOut; ! Number of served customers;
Process Class IGenerator;
Begin
While true do begin
Hold(Uniform(MinInt(Period),MaxInt(Period),TrialSeedG));
Activate New ICustomer(Time); ! Interval between arrivals: ;
End While;
End of IGenerator;
Process Class ICustomer(Arrival); Real Arrival;
Begin
Ref(ICustomer) Next;
If not Queue.Empty or (BusyServers >= Servers) then
Wait(Queue); ! Has to wait in Queue;
! Service can start;
BusyServers := BusyServers + 1;
Hold(Normal(S1Mean, S1Std, TrialSeedS)); ! Teller's service;
BusyServers := BusyServers - 1;
If not Queue.Empty then begin
Next :- Queue.First;
Next.Out; ! First from Queue served;
Activate Next after Current;
End If;
CustOut := CustOut + 1;
TotTime := TotTime + Time - Arrival;
End of ICustomer;
! Internal MAIN program body;
TrialSeedG := 7; ! Seeds for random variables;
TrialSeedS := 23;
Servers := Trial;
TrialDuration := 600;
Queue :- New Head;
Activate New IGenerator;
Hold(TrialDuration); ! Internal experiment duration;
TimeSpent(Trial) := TotTime/CustOut;
OutInt(Trial,13);
OutFix(TimeSpent(Trial),3,23); OutImage;
End of internal simulation;
! ********************************************************** ;
OutText("Enter the number of tellers : "); OutImage;
Tellers := InInt;
OutText("Enter the number of cashiers : "); OutImage;
Cashiers := InInt;
Hold(Duration(Period));
Report;
OutText("Press Enter to Continue."); OutImage; InImage;
End For;
End of program;
Ez a szimuláció eredménye, a megadott számokkal együtt. Összesen 6 munkatársunk van, az ügyintézők és a pénztárosok beosztását a felhasználó adja meg. Figyeljük meg a legnagyobb rendszerben eltöltött időt. Egészen a harmadik periódusig elfogadható szinten marad, amikoris viszont 63.93 percre emelkedik (meg kell említenünk, hogy a teljes kiszolgálási idők átlaga 6+8=14 perc). Így világos, hogy a harmadik, nagyon leterhelt periódusban eggyel több ügyintéző érezhetően javítaná a rendszer teljesítményét. Az elméletet egy ugyanezen adatokkal történő újabb futtatással ellenőriztük 4 ügyintéző és 3 pénztáros mellett. Ez a következő eredményeket adta: a rendszerben töltött átlagos idő 19.67 perc ( 21.84 perc két pénztárossal), a rendszerben töltött leghosszabb idő pedig 36.58 percre csökkent, ahogy azt vártuk. A szimuláció végkövetkeztetéseképp tehát azt javasolja a vezetőségnek, hogy a harmadik periódusban eggyel több ügyintézőt osszanak be, máskor pedig a rendszer jól teljesít 6 munkatárssal is.
*** Results of internal simulation *** Period 1
Tellers Average time spent
1 181.404
2 52.691
3 6.132
4 5.979
5 5.972
6 5.972
Enter the number of tellers :
3
Enter the number of cashiers :
3
*** Report on external simulation ***
42 customers ready at time 120.00
Average time in system: 18.52
Maximum time in system: 25.95
Press Enter to Continue.
*** Results of internal simulation *** Period 2
Tellers Average time spent
1 36.620
2 6.090
3 6.045
4 6.038
5 6.038
6 6.038
Enter the number of tellers :
2
Enter the number of cashiers :
4
*** Report on external simulation ***
91 customers ready at time 360.00
Average time in system: 17.29
Maximum time in system: 27.16
Press Enter to Continue.
*** Results of internal simulation *** Period 3
Tellers Average time spent
1 205.290
2 103.226
3 7.937
4 5.993
5 5.974
6 5.972
Enter the number of tellers :
4
Enter the number of cashiers :
2
*** Report on external simulation ***
119 customers ready at time 480.00
Average time in system: 21.84
Maximum time in system: 63.93
Press Enter to Continue.