Az A+ programozási nyelv

Függvények

Függvények, eljárások

Monadikus skalár függvények

Négy kategóriába sorolhatók:
Használatuk és az eredmény:

Minden monadikus függvény skalárról skalárra képez. Az argumentum minden elemére a többi elemtől függetlenül történik a leképezés.

A függvények leírása angol ábécé szerinti sorrendben:

Absolute value - abszolút érték: | X

Az argumentum és az eredmény mind egyszerű numerikus tömbök.
A paraméterül kapott tömb minden egyes elemének az abszolút értékét képezi.

Példa:

| 12.3 -3 12.3 3

Ceiling - felső egész rész: Óx

Az argumentum egy numerikus tömb, az eredmény minden esetben egész számokot tartalmazó, az argumentum hosszúságával megegyező tömb.
Az argumentum minden elemének a felső egész részét képezi.

Példa:

Ó10 10.2 10.5 10.98 -9 -9.2 -9.5 -9.98 10+1e-13 10 11 11 11 -9 -9 -9 -9 10

Exponential - exponenciális függvény: *x

Az argumentum és az eredmény is numerikus függvények. Az eredmény minden esetben lebegő pontos számokat tartalmaz.
Az argumentum minden egyes elemére alkalmazza az exponenciális függvényt.

Példa:

*-1 0 1 2 710 .3678794412 1 2.718281828 7.389056099 Inf

Floor - alsó egész rész: Äx

Az argumentum egy numerikus tömb, az eredmény minden esetben egész számokat tartalmazó, az argumentum hosszúságával megegyező tömb.
Az argumentum minden elemének alsó egész részét képezi.

Példa:

Ä10 10.2 10.5 10.98 -9 -9.2 -9.5 -9.98, 10-1e-13 10 10 10 10 -9 -10 -10 -10 10

Identity - identitás: +x

Az argumentum és eredmény típusa megegyezik. Az eredmény minden esetben a függvény argumentuma.

Példa:

+'abc' abc

Natural log - természetes logaritmus: ðx

Az argumentum és az eredmény egy tömb. Az argumentum minden eleme nem negatív szám. Az eredmény minden esetben lebegőpontos szám.
Az argumentum minden elemének a természetes logaritmusával tér vissza.

Példa:

ð 1 10 100 0 0 2.302585093 4.605170186 -Inf

Negate - negálás: -x

Az argumentum és az eredmény numerikus tömb.
Az argumentum minden elemének az additív inverzét adja eredményül.

Példa:

- 23 -2 45 0 -1 .5 -23 2 -45 0 1 -0.5

Not - not: ~x

Az argumentum és az eredmény mind egyszerű tömbök. Az eredmény elemeinek típusa egész szám.
Amennyiben egy elem elég közel van a nullához(1e-13), az eredmény 1, minden más esetben 0.

Példa:

~0 1 1 0

Példa:

~-1 0 1 2 3 0 1 0 0 0

Pi times - Pi-szeres: Ïx

Az argumentum és az eredmény mind egyszerű tömbök. Az eredmény elemeinek típusa minden esetben lebegőpontos szám.
Minden elem Pi-szeresét adja eredményül.

Példa:

Ï1 2 .5 1e308 3.141592654 6.283185307 1.570796327 Inf

Reciprocal - reciprok: ßx

Az argumentum és az eredmény egyszerű tömbök. Az eredmény elemeinek típusa lebegőpontos szám.
Az argumentum elemeinek reciprokát gyártja le.

Példa:

ß .5 1.5 -2 100 0 -1e-309 2 0.6666666667 -0.5 0.01 Inf -Inf

Roll - roll: ?x

Az argumentum és az eredmény egyszerű tömbök. Az eredmény minden esetben egész szám.

Példa:

?20Ò10 3 4 7 2 1 5 0 1 7 0 7 9 9 6 9 3 9 0 0 6 ?20Ò10 2 9 2 4 5 1 3 5 8 3 0 3 7 8 6 9 5 8 0 4

Sign - előjel: «x

Az argumentum és az eredmény mind egyszerű tömbök. Az eredmény elemeinek típusa minden esetben egész szám.
Ha az argumentum elemének értéke negatív, az eredmény -1 lesz, nulla esetén 0, pozitív számok esetén +1.

Példa:

« 100 -2.5 0 5 -Inf 1 -1 0 1 -1


Diadikus skalár függvények



Osztályozásuk:

Használatuk:


Minden diadikus függvény skalárról skalárra képez. Az argumentum minden elemét a többitől függetlenül dolgozza fel.

1.
Amennyiben az argumentumok alakja megegyező, az eredmény alakja az argumentumok alakjával megegyező lesz, és az eredmény elemei az argumentumok megfelelő elemeinek az adott diadikus függvénnyel vett értékei lesznek.


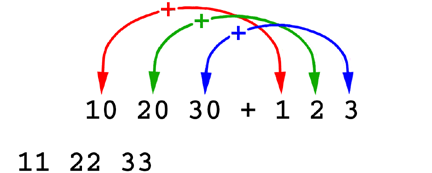
2.
Ha az egyik argumentum mindössze egy elemből áll(singleton), az eredmény elemei a másik argumentum és a signleton elem adott függvénnyel vett értékei lesznek. Az eredmény alakja megegyezik a nem egyelemű argumentum alakjával.

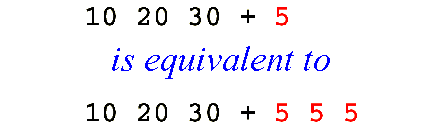
tehát:


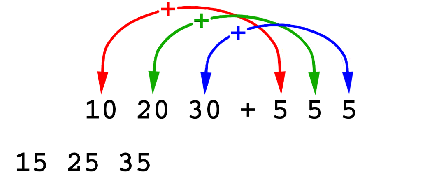
3.
Amennyiben mindkét argumentum egyelemű, az eredmény is egyelemű lesz.

A diadikus függvények felsorolása az angol ábécé szerinti sorrendben:



Add - összeg : y+x

Az argumentumok és az eredmény is egyszerű numerikus tömbök. Ha mindkét argumentum, amik nem üresek, és egész értékeket tárolnak, az eredmény is egész elemeket tároló tömb lesz, feltéve, hogy az elemek mind ábrázolhatóak integer-ként, ellenkező esetben lebegőpontos számként kerülnek ábrázolásra. Amennyiben az egyik argumentum üres, és ennek az argumentumnak lehetséges elemei lebegőpontos számok, az eredmény is lebegőpontos értékeket tartalmaz, minden más esetben a nem üres argumentum típusával egyezik meg az eredmény típusa. Ha mindkét argumentum üres, és az egyik elemeinek típusa lebegőpontos, a másiknak pedig egész, az eredmény elemeinek típusa is lebegőpontos lesz, az eredmény típusa minden más esetben a jobb oldali argumentum típusával egyezik meg.
Az eredmény elemei az argumentumok megfelelő elemeinek összege.

Példa:

-1 0 1 1e308 + 10 20 30 1e308 9 20 31 Inf

And - és : y^x

Az argumentumok és az eredmény egész típusú tömbök.
Amennyiben x és y logikai értékek(0 és 1), y^x eredménye a logikai ÉS-sel vett eredménye x-nek és y-nak. Azaz 1^1 eredménye 1, 0^1, 1^0, és 0^0 eredménye 0 lesz.
Az And függvény szigorúan logikai értékekkel számol, és minden nem nulla elemet úgykezel, mintha 1 lett volna az értéke.

Példa:

0 0 1 1 ^ 0 1 0 1 0 0 0 1

Példa:

43 ^ 14 1

Circle - trigonometrikus kompozíció yÏx:

Az argumentumok és az eredmény egyszerű numerikus tömbök, de a bal oldali argumentum akár szimbolikus is lehet. Az eredmény elemei minden esetben lebegőpontos értékek. Amennyiben a bal oldali argumentum értékei egészek, azok értéke -7 és 7 közt kell hogy legyen.
A+ beli kifejezésJelentés
sinarccos o x vagy 0 o x (1-x*2)*0.5
sin o x vagy 1 o x sin x
cos o x vagy 2 o x cos x
tan o x vagy 3 o x tan x
secarctan o x vagy 4 o x (1+x*2)*0.5
sinh o x vagy 5 o x sinh x
cosh o x vagy 6 o x cosh x
tanh o x vagy 7o x tanh x
arcsin o x vagy -1 o x arcsin x
arccos o x vagy -2 o x arccos x
arctan o x vagy -3 o x arctan x
tanarcsec o x vagy -4 o x (-1+x*2)*0.5
arcsinh o x vagy -5 o x arcsinh x
arccosh o x vagy -6 o x arccosh x
arctanh o x vagy -7 o x arctanh x

Példa:

1 1 3 -3 Ï Ïß2 4 2 0 ã sin(pi/2), sin(pi/4), tan(pi/2), arctan(Inf) 1 0.7071067812 1.633177873e+16 1.570796327

Combine Symbols - kompozíció yÖx:

Az argumentumok és az eredmény szimbólumok tömbje.
Az argumentumok elemeinek páronként veszi a kompozícióját.

Példa:

`b.c `a Ö `x `y `b.c.x `a.y

Divide - tört yßx:

Az argumentumok és az eredmény numerikus tömbök, az eredmény elemeinek típusa minden esetben lebegőpontos.
y elemeit x megegyező indexű elemeivel osztja. Amennyiben az osztó elem értéke nulla, az eredmény egy egyedi skalár érték, Inf lesz, ha pedig az osztandó elem negatív, az eredmény -Inf.

Példa:

0 1 2 3 4 -5ß2 2 2 2 0 0 0 0.5 1 1.5 Inf -Inf

Equal to - egyenlő y=x:

Az argumentumok típusa bármi lehet, az eredmény elemeinek típusa logikai. Amennyiben az argumentumok megfelelő értékei egyenlőek, az ezeknek megfeleltetett elem értéke 1 lesz, ellenkező esetben 0.

Példa:

' '='this is it' 0 0 0 0 1 0 0 1 0 0

Példa:

(<2 3, 4+1e-13)=(2 3 4;'abcde';É5 6) 1 0 0

Példa:

1 2 3 = '123' 0 0 0

Greater than - nagyobb mint y>x:

Az argumentumok egyszerű numerikus, karakter és szimbólumok tömbje lehet, az eredmény logikai értékek tömbje(egész értékekkel reprezentálva az igaz - 1 és hamis - 0 értékeket ).
A megfelelő elempárokhoz rendelt érték 1 lesz, ha y nagyobb mint x, ellenkező esetben pedig 0. A karakterek az ASCII kódjuk alapján kerülnek összehasonlításra, a szimbólumok pedig a neveik szerinti ábécé sorrendben.

Példa:

(-200 0 90 100 101 200,(100+1e-12),100+1e-11)>100 0 0 0 0 1 1 0 1

Példa:

'b' > 'abc' 1 0 0

Példa:

'B' > 'abc' ã ASCII, not English, order. 0 0 0

Példa:

`b > `a`b`c 1 0 0

Példa:

`B > `a`b`c ã Likewise. 0 0 0

Példa:

`pint > `cup `pints `pound `quart `snootful `gallon 1 0 0 0 0 1

Greater than or Equal to - nagyobb vagy egyenlő y¦x:

Az argumentumok egyszerű numerikus, karakter és szimbólumok tömbje lehet, az eredmény logikai értékek tömbje(egész értékekkel reprezentálva az igaz - 1 és hamis - 0 értékeket ).
A megfelelő elempárokhoz rendelt érték 1 lesz, ha y nagyobb vagy egyenlő mint x, ellenkező esetben pedig 0. A karakterek az ASCII kódjuk alapján kerülnek összehasonlításra, a szimbólumok pedig a neveik szerinti ábécé sorrendben.

Példa:

-200 0 90 100 101 200¦100 0 0 0 1 1 1

Less than - kisebb mint y<x:

Az argumentumok egyszerű numerikus, karakter és szimbólumok tömbje lehet, az eredmény logikai értékek tömbje(egész értékekkel reprezentálva az igaz - 1 és hamis - 0 értékeket ).
A megfelelő elempárokhoz rendelt érték 1 lesz, ha y kisebb mint x, ellenkező esetben pedig 0. A karakterek az ASCII kódjuk alapján kerülnek összehasonlításra, a szimbólumok pedig a neveik szerinti ábécé sorrendben.

Példa:

-200 0 90 100 101 200<100 1 1 1 0 0 0

Less than or Equal to - kisebb vagy egyenlő y¤x:

Az argumentumok egyszerű numerikus, karakter és szimbólumok tömbje lehet, az eredmény logikai értékek tömbje(egész értékekkel reprezentálva az igaz - 1 és hamis - 0 értékeket ).
A megfelelő elempárokhoz rendelt érték 1 lesz, ha y kisebb vagy egyenlő mint x, ellenkező esetben pedig 0. A karakterek az ASCII kódjuk alapján kerülnek összehasonlításra, a szimbólumok pedig a neveik szerinti ábécé sorrendben.

Példa:

-200 0 90 100 101 200¤100 1 1 1 1 0 0

Log - logaritmu yðx:

Az argumentumok és az eredmény egyszerű numerikus tömbök. Az eredmény elemeinek típusa minden esetben lebegőpontos.
A függvény az x elemeinek a logaritmusát veszi y bázissal.

Példa:

10ð.1 1 10 100 1000 1234.5 0 -1 0 1 2 3 3.091491094 -Inf

Max - maximum yÓx:

Az argumentumok és az eredmény egyszerű numerikus tömbök. Ha mindkét argumentum, amik nem üresek, és egész értékeket tárolnak, az eredmény is egész elemeket tároló tömb lesz, ellenkező esetben az elemek lebegőpontos számként kerülnek ábrázolásra. Amennyiben az egyik argumentum üres, és ennek az argumentumnak lehetséges elemei lebegőpontos számok, az eredmény is lebegőpontos értékeket tartalmaz, minden más esetben a nem üres argumentum típusával egyezik meg az eredmény típusa. Ha mindkét argumentum üres, és az egyik elemeinek típusa lebegőpontos, a másiknak pedig egész, az eredmény elemeinek típusa is lebegőpontos lesz, az eredmény típusa minden más esetben a jobb oldali argumentum típusával egyezik meg.
Az eredmény y, amennyiben y nagyobb mint x, ellenkező esetben x az eredmény.

Példa:

0 Ó 3 .5 -1 5 -.1 3 .5 0 5 0

Min - minimum yÄx:

Az argumentumok és az eredmény egyszerű numerikus tömbök. Ha mindkét argumentum, amik nem üresek, és egész értékeket tárolnak, az eredmény is egész elemeket tároló tömb lesz, ellenkező esetben az elemek lebegőpontos számként kerülnek ábrázolásra. Amennyiben az egyik argumentum üres, és ennek az argumentumnak lehetséges elemei lebegőpontos számok, az eredmény is lebegőpontos értékeket tartalmaz, minden más esetben a nem üres argumentum típusával egyezik meg az eredmény típusa. Ha mindkét argumentum üres, és az egyik elemeinek típusa lebegőpontos, a másiknak pedig egész, az eredmény elemeinek típusa is lebegőpontos lesz, az eredmény típusa minden más esetben a jobb oldali argumentum típusával egyezik meg.
Az eredmény y, amennyiben y kisebb mint x, ellenkező esetben x az eredmény.

Példa:

99.5 100 91.1 112 99 Ä 100 99.5 100 91.1 100 99

Multiply - szorzat y«x:

Az argumentumok és az eredmény is egyszerű numerikus tömbök. Ha mindkét argumentum, amik nem üresek, és egész értékeket tárolnak, az eredmény is egész elemeket tároló tömb lesz, feltéve, hogy az elemek mind ábrázolhatóak integer-ként, ellenkező esetben lebegőpontos számként kerülnek ábrázolásra. Amennyiben az egyik argumentum üres, és ennek az argumentumnak lehetséges elemei lebegőpontos számok, az eredmény is lebegőpontos értékeket tartalmaz, minden más esetben a nem üres argumentum típusával egyezik meg az eredmény típusa. Ha mindkét argumentum üres, és az egyik elemeinek típusa lebegőpontos, a másiknak pedig egész, az eredmény elemeinek típusa is lebegőpontos lesz, az eredmény típusa minden más esetben a jobb oldali argumentum típusával egyezik meg.
Az eredmény elemei az argumentumok megfelelő elemeinek szorzata.

Példa:

10«0 1 2 3 1e308 0 10 20 30 Inf

Not equal to - nem egyenlő y¨x:

Az argumentumok típusa bármi lehet, az eredmény elemeinek típusa logikai. Amennyiben az argumentumok megfelelő értékei egyenlőek, az ezeknek megfeleltetett elem értéke 1 lesz, ellenkező esetben 0.

Példa:

''¨'this is it' 1 1 1 1 0 1 1 0 1 1

Példa:

(<2 3, 4+1e-13)¨(2 3 4;'abcde';É5 6) 0 1 1

Példa:

1 2 3 ¨ '123' 1 1 1

Or - vagy y©x:

Az argumentumok és az eredmény egész típusú tömbök. Amennyiben x és y logikai értékek(0 és 1), y^x eredménye a logikai ÉS-sel vett eredménye x-nek és y-nak. Azaz 0©0 eredménye 0, 0©1, 1©0, és 1©1 eredménye 1 lesz.
Az And függvény szigorúan logikai értékekkel számol, és minden nem nulla elemet úgykezel, mintha 1 lett volna az értéke.

Példa:

0 0 1 1©0 1 0 1 0 1 1 1

Példa:

43©14 1

Power - hatvány y*x:

Az argumentumok tetszőleges numerikus tömbök, az eredmény minden esetben lebegőpontos elemeket tároló tömb. A hatványfüggvény y elemeinek veszi az x-ben azoknak megfeleltetett elemek szerinti hatványát.

Példa:

2 * 0.5 1 2 3 4 5 6 7 8 1025 1 1.414213562 2 4 8 16 32 64 128 256 Inf

Residue - osztási maradék y|x:

Az argumentumok és az eredmény is egyszerű numerikus tömbök. Ha mindkét argumentum, amik nem üresek, és egész értékeket tárolnak, az eredmény is egész elemeket tároló tömb lesz, ellenkező esetben lebegőpontos számként kerülnek ábrázolásra. Amennyiben az egyik argumentum üres, és ennek az argumentumnak lehetséges elemei lebegőpontos számok, az eredmény is lebegőpontos értékeket tartalmaz, minden más esetben a nem üres argumentum típusával egyezik meg az eredmény típusa. Ha mindkét argumentum üres, és az egyik elemeinek típusa lebegőpontos, a másiknak pedig egész, az eredmény elemeinek típusa is lebegőpontos lesz, az eredmény típusa minden más esetben a jobb oldali argumentum típusával egyezik meg.
Az eredmény elemei az argumentumok megfelelő elemeinek osztási maradéka. Speciálisan Inf | x és -Inf | x eredménye minden x-re 0.

Példa:

100 | 1930 1941 1952 1978, 100+1e-12 30 41 52 78 0

1.4 1.4 -1.4 -1.4 | 3.7 -3.7 3.7 -3.7
0.9 0.5 -0.5 -0.9

Subtract - különbség y-x:

Az argumentumok és az eredmény is egyszerű numerikus tömbök. Ha mindkét argumentum, amik nem üresek, és egész értékeket tárolnak, az eredmény is egész elemeket tároló tömb lesz, feltéve, hogy az elemek mind ábrázolhatóak integer-ként, ellenkező esetben lebegőpontos számként kerülnek ábrázolásra. Amennyiben az egyik argumentum üres, és ennek az argumentumnak lehetséges elemei lebegőpontos számok, az eredmény is lebegőpontos értékeket tartalmaz, minden más esetben a nem üres argumentum típusával egyezik meg az eredmény típusa. Ha mindkét argumentum üres, és az egyik elemeinek típusa lebegőpontos, a másiknak pedig egész, az eredmény elemeinek típusa is lebegőpontos lesz, az eredmény típusa minden más esetben a jobb oldali argumentum típusával egyezik meg.
Az eredmény elemei az argumentumok megfelelő elemeinek különbsége.

Példa:

-1 0 99.5 1e308 - .5 -1 .5 -1e308 -1.5 1 99 Inf

Nemskalár primitív függvények


Osztályzásuk:

Ezek közül a fontosabbak:


Assignment - értékadás xûa és (x)ûa:

A jobb oldali argumentum egy tömb, vagy egy függvény-kifejezés. A bal oldali argumentum(target) egy érvényes változónév. Az értékadás explicit értéke 'a' értéke lesz, amennyiben 'a' egy tömb, különben pedig a függvény-kifejezés kiértékelés utáni értéke. A művelet mellékhatásaként 'a' értéke átadódik 'x'-nek.
Az értékadás jobb oldalán nem állhat tisztán egy operátor.
Több egyszerű értékadás is elvégezhető egyszerre:

Példa:

(a;c.b;f;d;d)û('ABC';10+É3 4;+.«;2;5)
Ebben az esetben az értékadás jobb oldalán lévő kifejezések a nekik megfelelő bal oldalon lévő operandusoknak adódnak páronként át. A példában 'f' egy skalár függvény lesz, nem pedig egy egyszerű függvény. Az értékadás hatására d értéke 5lesz.
Replicate - ismétlés y/x:

y egy egyszerű nemnegatív egészeket tároló vektor, x pedig egy tetszőleges tömb. Amennyiben y elemeinek száma nagyobb 1-nél, akkor elemeinek száma meg kell egyezzen x elemeinek számával. A / bal oldalán álló argumentumot szokás maszkvektornak is nevezni.
A maszkvektor minden egyes eleme a másik argumentumban neki megfelelő elemet ismétli meg az eleme értéke szerint.

Példa:

0 0 1 0 2 / `a `b `c `d `e `c `e `e

Megjegyzés: ez az operátor kiváltja a nem vektor-orientált nyelvekbeli if és for használatát.

Példa:

egy adott számsorozatból határozzuk meg a -10 és 10 köztieket: ( 10 <= |x )/x û 3 16 -2 8 15 4 -10
először 'x' értékül kapja a jobb oldali vektorta zárójelben lévő kifejezés a feltételnek megfelelően kiértékelődik:
1 0 1 1 0 1 1
végül pedig végrehajtódik a következő egyszerű művelet: 1 0 1 1 0 1 1 / 3 16 -2 8 15 4 -10
a végeredmény: 3 -2 8 4 -10

Find - keresés yÉx:

Az argumentumok tetszőleges típusú tömbök lehetnek, azonban 'y' elemeinek rangja nem lehet nagyobb 'x' rangjánál. Az eredmény tömbjének alakja megegyezik az 'x'-ből az utolsó 's' dimenzió elhagyásának alakjával, ahol 's' az 'y' elemeinek rangja.
A keresés függvény a második argumentumban megadott elemek első argumentumbeli első előfordulásának az indexét határozza meg.
Amennyiben egy elem nem található meg, az index értéke a második argumentum rangja lesz.

Példa:

2 2 3 2 7 1 É 1 2 5 5 0 6

Choose - kiválasztás y#x:

A bal oldali argumentum egy egészeket tartalmazó tömb, a jobb oldali pedig egy tetszőleges tömb. 'y' rangja kisebbnek kell lennie, mint 'x' elemeinek rangja.
Az eredménybe 'x'-ből az 'y'-ban megadott indexű elemek kerülnek be.

Példa:

3 # `a `b `c `d `e `d

Példa:

Adott egy azonosítókból álló 'a' vektor és egy tetszőleges 'b' vektor, ami az azonosítókhoz tartozóértéket tartalmazza. Írjuk ki a 4-es azonosítóhoz tartozó értéket!
a: 1 3 4 5 7 b: `v `t `a `g
`f kifejezés : (a É 4) # b
eredmény : `a