Egy teljes példa
Ebben a fejezetben egy egyszerű példán keresztül bemutatásra kerül, hogy hogyan modellezzünk egy problémát GAMS-ban, illetve hogyan használjuk a korábbi fejezetekben megismert nyelvi eszközöket.
A feladat algebrai specifikációja
Adott két gyár, három felvevőpiac, és feladatunk az áru minimális költségek melletti leszállítása. Tehát az indexek legyenek:
- i = gyárak
- j = piacok
Adott paraméterek:
- ai = az i-edik gyár termelése konténerben
- bj = a j-edik piac igénye konténerben
- di,j = az i-edik gyár és a j-edik piac közötti távolság ezer mérföldben
- ci,j = az egységnyi áru szállítási költsége az i-edik gyár és a j-edik piac között (dollár/konténer/ezer mérföld)
Döntési változók:
- xi,j = a leszállított árumennyiség konténerekben az i-edik gyárból a j-edik piacra
- termelési limit az i-edik gyárnál:
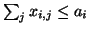(minden szóba jövő i-re) - igény a j-edik piacon:
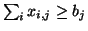(minden szóba jövő j-re)
A célfüggvény pedig:
Megoldás GAMS-ban
Az alábbi GAMS kód reprezentálja a fentebb vázolt feladat megoldását.
SETS
I canning plants / Seattle, San-Diego /
J markets / New-York, Chicago, Topeka /
;
PARAMETERS
A(i) capacity of plant i in cases
/ Seattle 350
San-Diego 600 /
B(j) demand market j in cases
/ New-York 325
Chicago 300
Topeka 275 /
;
TABLE D(i,j)
distance in thousands of miles
New-York Chicago Topeka
Seattle 2.5 1.7 1.8
San-Diego 2.5 1.8 1.4
;
SCALAR F
'freight in dollars/case/thousand miles'
/ 90 / ;
PARAMETER C(i,j)
transport cost in thousands of dollars per case;
c(i,j) = F * d(i,j) / 1000 ;
VARIABLES
X(i,j) shipment quantities in cases
Z total transp. costs in thousands of dollars
;
POSITIVE VARIABLE x;
EQUATIONS
COST define objective function
SUPPLY(i) observe supply limit at plant i
DEMAND(j) satisfy demand at market j
;
cost ..
z =e= sum((i,j), c(i,j) * x(i,j)) ;
supply(i) ..
sum(j, x(i,j)) =l= a(i) ;
demand(j) ..
sum(i, x(i,j)) =g= b(j) ;
MODEL transport
/ all / ;
SOLVE transport USING LP MINIMIZING z ;
A megoldás értelmezése
Ismétlésül tekintsük át az egyes sorok, utasítások jelentését!
- sets
- - GAMS-ban természetes módon adhatunk meg indexeket (halmazokat): deklaráljuk és megnevezzük a halmazt, majd felsoroljuk az elemeit.
- parameters
- - itt az adatokat indexelt paraméterként adtuk meg, az
értékeket egyszerűen felsoroltuk.
A paraméter neve után megadhatunk magyarázó szöveget (a fenti példában kisbetűkkel szedve), amelyek segítik a felhasználót, illetve automatikusan belekerülnek a kimeneti fájlokba, a megfelelő helyekre. - table
- - adatokat kényelmesen megadhatunk táblázatokba szedve is, ekkor ügyelnünk kell a tördelésre.
- scalar
- - konstansokat deklarálhatunk skalárként, megadva az értékét.
- parameter
- - (adatmódosítás) ha az adatokat számítással szeretnénk megadni, akkor előbb deklaráljuk a megfelelő paramétert, majd adjuk meg a számítási formulát, amely - indexelt paraméter esetén - minden lehetséges indexértékre kiszámítódik.
- variables
- - döntési változók megadása, algebrai módon, az esetleges indexükkel megadva, alapértelmezett a free variable, ez megváltoztatható később is.
- equations
- - a célfüggvényt és az egyes változókra tett megszorításokat lehet itt előbb deklarálni, majd specifikálni.
- model
- - a modell nevének egyedinek kell lennie, és megadhatjuk, mely
egyenlőségeket szeretnénk belevenni modellünkbe. Az all kulcsszóval
minden egyenlőséget beletettünk a modellbe, ami ekvivalens a
MODEL transport / cost, supply, demand / ;utasítással.
- solve
- - megadjuk a megoldandó modellt (transport), kiválasztjuk a solvert (LP), az optimalizálás irányát (minimizing) és a célváltozót (z).