Többirányú elágazások
A nyelv támogatja a többirányú (case-szerű) elágazásokat. Az elágazás blokk megkap egy értéket, amelytől függően kell valamit csinálnia.
Az értékhez tartozó blokk lefut, majd az eredményekkel továbbszámolhatunk. Akár szám, szöveg, logikai, esetleg enum típusú elemek alapján
ágazhatunk el. Lényeges, hogy a típus tetszőleges értékéhez tudjon mit csinálni az elágazás. Emiatt vezették be a Default értéket,
ami tetszőleges olyan érték esetén fut le, mely esetén az elágazás más ága nem aktivizálódhat. Egy ág több érték esetén is aktivizálódhat,
ekkor az értékeket felsorolhatjuk, vesszővel elválasztva. Egész számok esetén intervallumok is megadhatók. A 3..7 címkével ellátott ág tetszőleges,
az alsó határ, és a felső határ közötti értéket felvevő érték (a határokat is beleszámítva) esetén aktivizálódik. A ..5, illetve az 5.. esetén az alsó,
illetve a felső határ nincs megadva, azaz első esetben tetszőleges felső határnál kisebb, vagy vele egyenlő, míg második esetben az alsó határnál nagyobb,
vagy egyenlő értékek esetén aktivizálódik az ág. Az intervallumok, és az értékfelsorolások kombinálhatók, azaz megengedett egy ágnak
3..7, 12, 24.. aktiválási feltételt adni. A LabVIEW-ben egyszerre csak egy ág aktivizálódhat.
Az elágazások a blokk diagramban egy téglalapként jelennek meg. A téglalap tetején választhatjuk ki, aktuálisan melyik ág látszódjon.
A téglalap szélén látható ? jelhez kapcsolhatjuk azt a vezetéket, amelyen futó érték meghatározza, hogy melyik ágon folytatódjon a program futása.
Ebből a jelből továbbvezetve egy vezetéket a case struktúrában lekérdezhetjük például a Default ágban az értéket. A kereten elhelyezhetők kis téglalapok,
amelyek segítségével egyéb, számoláshoz szükséges vezetékek csatlakozhatnak a case szerkezethez, mind bemenetiek, mind kimenetiek.
Mivel a kimenetekből kiinduló vezetékek túlsó végei pontosan egy eredményt várnak, ezért a case struktúra belsejében biztosítani kell azt,
hogy minden ág esetén az összes értéket váró vezetékre kerüljön is érték. Az egyes ágak belsejében tetszőleges programszerkezetek megvalósíthatók.
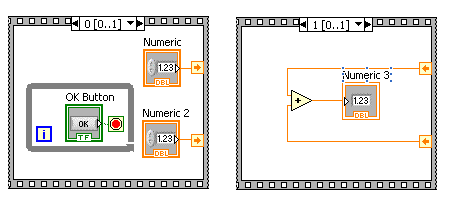
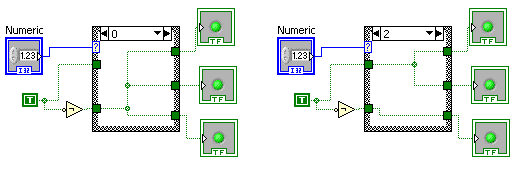
Példaként bemutatok egy mintakódot, amely egy egész szám bemenettől függően kapcsolgat három led lámpát. A könnyebbség kedvéért kiemeltem
az elágazáson kívülre a TRUE konstanst, így magában az elágazásban most csak vezetékek vannak. Az ábrán a 0, illetve a 2 eset látható.
While ciklus
Lehetőségünk van feltételig futó ciklusokat létrehozni a programainkban. A ciklus keretén belül található egy megállási feltételt váró ikon. Ha ez az ikon a hozzákötött vezetéken TRUE értéket kap, akkor a ciklus futása megáll. Tehát, a ciklus egy hátultesztelő, repeat-until ciklushoz hasonlít a legjobban. A ciklus lefutásának sorszáma is lekérdezhető. A sorszámozán 0-tól kezdődik. Ezt egy i betűt tartalmazó kék négyzet kinézetű ikon biztosítja. Az elágazásokhoz hasonlóan, megadható a ciklusnak bemenő érték, illetve visszatérési értékek is, melyek a ciklus utolsó lefutása során adódnak ki.
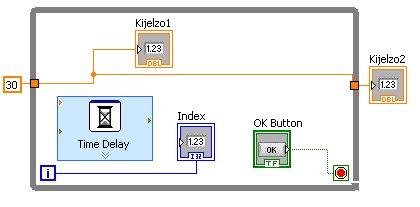
A példában látható egy ciklus. A Time Delay függvény 1 másodperces várakozásra van beállítva. Tehát, a ciklus futása során az Index nevű megjelenítő 0-tól indulva, másodpercenként növeli az értékét. A ciklus futása az OK gomb megnyomásakor fejeződik be. A Kijelzo1 a ciklus futásának kezdetén megkapja a kijelzendő 30 számkonstanst, míg a Kijelzo2 csak az OK gomb megnyomása után kapja meg az értékét. A ciklusag mindig teljes egészében lefut, ígyhát a jelen esetben biztosan egész számú másodpercig fog futni, függetlenül attól, hogy az OK gomb pontosan mikor lett lenyomva. Ha a ciklusfeltétel igaz a ciklusmag lefutásának pillanatában, akkor többet már nem fog lefutni a ciklus.
For ciklus
A For ciklus hasonlóan működik a while ciklushoz. A különbség, hogy nincs megállási feltétele. Ehelyett a bal felső sarokban található N betűt tartalmazó ikonnal adható meg, hogy hánysor fusson le a ciklusmag. Ez az érték a cikluson belül is lekérdezhető. A cikluslefutás sorszáma hasonlóan kérdezhető le, mint a while ciklus esetében. Ha a lefutások száma N, akkor az egyes lefutásokkor 0,…,N-1 értékeket kapjuk meg az egyes ciklusmag lefutásokkor.
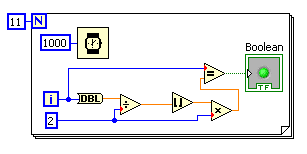
A mintaprogram villog a leddel. Egy másodpercig ég, majd egy másodpercig nem ég. A villogást egy egyszerű feltétellel oldottam meg: Vizsgálom, hogy a ciklusváltozó fele alsó egészrészének kétszerese egyenlő-e a ciklusváltozóval. Ha ez teljesül, akkor páros sorszámú iterációt hajtjuk végre, ég a led, különben pedig nem ég. Látható a programban egy int-double típuskonverzió, illetve a piros pontocskák jelzik az automatikus konverziókat.
Shift regiszter
Érdekes lehet, hogy az egyes ciklus iterációban kiszámolt értéket a következő iterációban is le tudjuk kérdezni. Ezt biztosítják a Shift regiszterek. Egy fibonacci-számokat számoló programon keresztül mutatom be a működésüket:
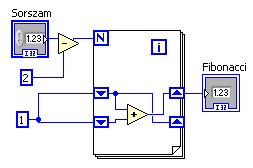
A ciklus falán található lefele nyilacskák tartalmazzák a korábbi iterációk értékét, amit a ciklusmagban le tudunk kérdezni. Ezeknek nyilván kell a cikluson kívülről kezdőértéket adni. Velük egy magasságban, a ciklus túloldalán található felfele nyilacskák kapják meg a shift regiszterek következő iteráció-beli értékét. A program 1-re, illetve 2-re 1-et ad vissza, és ekkor a ciklusmag egyszer sem fut le. 3, vagy nagyobb értékű bemenetre pedig a feljebb található shift regiszter bemenetén kapjuk az N+2. fibonacci számot, míg az alsó shift regiszter tárolja az N+1. sorszámút. Ezek összeadásával kapható meg az N+3. fibonacci szám. Tehát, a két shift regiszter mindig az előző két fibonacci számot tárolja, amiből a következő egyszerűen kiszámolható. Végül, a ciklus lefutása után megjelenik a képernyőn a keresett szám.
Tömbkimenetű ciklusok
A ciklusok minden egyes iterációjának egyes számolási eredményeit tömbbe fűzhetjük. Ezzel viszonylag egyszerűen generálhatók tömbök. Például, az XY Graph két tömbnek az összefűzését várja paraméterként. Az egyik tömb tárolja az X, míg a másik az Y koordinátákat.
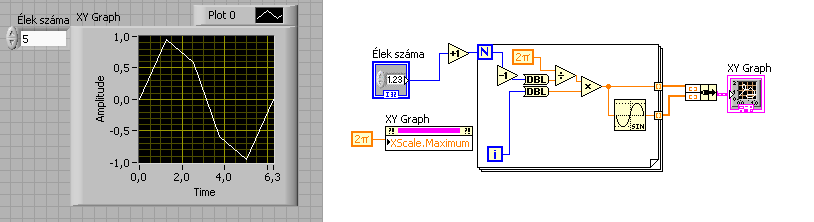
Látható, hogy a for ciklusban minden iterációban legeneráltuk az x pontokat, illetve az y pontokat. Ezek a cikluson kívül, mind tömbök jelennek meg. A blokk diagram bal alsó sarkában az XY Graph egy adattagját állítottuk be, hogy a függvény kitöltse széltében a grafikont. Hasonlóan, minden egyes grafikai objektumnak számtalan tulajdonsága beállítható, illetve lekérdezhető.
Szekvencia
Egy LabVIEW-ben írt program tele van párhuzamosságokkal. Ezek korlátozására találták ki a szekvenciákat. Tetszőleges függvény, illetve egyéb egység akkor adja vissza a
visszatérési értékeit, amikor minden lefutott benne. A szekvenciának is ez a lényege: Ha egy művetek elvégzése során sorrendiséget akarunk meghatározni, akkor ezt szekvenciával megtehetjük.
Példaként képzeljünk el egy olyan programot, amely valamely, esetleg bonyolult számítást egy gomb megnyomásakor kezd el. A bemenő adatok tetszőlegesen változtathatók, majd,
megnyomva a „Számolj!” gombot, megkapjuk az eredményt. A példakód egy sima összeadáson mutatja be egy ilyen program működését. A szekvenciában egy ciklust is elhelyeztem,
ami a gomb megnyomására való várakozást biztosítja.
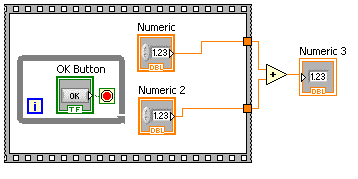
Nyilván, egy szekvencia általában több részből (frame) áll. A fenti programot is módosítani lehetne úgy, hogy az összegzés művelete a szekvencia következő részébe kerüljön. A szekvencia sorozat megjelenítését a blokkdiagramban kétféleképpen is megvalósíthatjuk. Kinézetre nem egyezik meg a két megvalósítás, de a működés tekintetében ugyanazt csinálja a kettő.
Flat Sequence
Ennek szép példája látható a mintakódban. Több frame esetén a kockák egymás után jelennek meg.
Stacked Sequence
Ebben az esetben a frame-k 0-tól kezdődően, természetes számokkal indexeltek. Egyszerre csak egy látszik belőlük, helytakarékosság szempontjából. Az egyes frame-k közötti váltás hasonlóan végezhető, mint elágazásokkor. A szekvenciában lokális változókat definiálhatunk, amik biztosítják az egymást követő frame-k közötti kapcsolatot. Ezeket a kereten elhelyezkedő kifele, illetve befele mutató nyilacskák jelzik. Egymást követő frame-k esetén két lokális változó ugyanaz, ha a keretnek azonos pontján helyezkedik el. A példában látható az összeadó program egy másik megvalósítása stacked sequence-vel: