
Bevezetés
A Mathematica 7-től kezdve a programban beépítve található meg a párhuzamos számítások elvégzéséhez szükséges eszközök, melyek teljes egészében leváltják a 6-os verzióig használt Parallel Computing Toolkit-et. A Mathematicában a párhuzamosságot egy mester Mathematica példány vezérli, ez felelős a többi kernel (dolgozó) folyamat indításáért és kezeléséért. A párhuzamossághoz szükséges funkciók nagy része a Mathematica nyelven van megvalósítva, így teljesen platformfüggetlen. A Mathematica párhuzamos lehetőségeinek a főbb tulajdonságai:- mester/szolga párhuzamosság
- Mathematica-ban íródott
- gép-független
- a távoli kernelekkel való kommunikáció MathLink felett történik
- a kernelek között szimbólumok is átadhatók (így függvények is például), nem csak számok és tömbök
- heterogén hálózatok, többprocesszoros gépek támogatása
- virtuális osztott memória, szinkronizáció
- párhuzamos funkcionális programozás és automatikus párhuzamosítás támogatása
Kapcsolódási lehetőségek
A Mathematicában számos megoldást implementáltak a kernelek közti adatcserére, egyaránt lehetőségünk van lokális és távoli gépeken futó kernelek közötti kapcsolat kialakítására. A különböző lehetőségek rövid ismertetése:- Helyi kernelek:
A kernelek a mester Mathematicával megegyező gépen futnak.
- Lightweight Grid:
A Lightweight Grid kapcsolódási módszer akkor használatos, ha a dolgozók a mester folyamattól eltérő gépeken futnak. Megfelelő megoldás heterogén hálózatokon, ahol nincs külön klaszterezési technológia.
- Cluster Integration:
Szintén akkor használatos, ha a mester és a dolgozók különböző gépeken futnak, azonban a hálózat gépein elérhető valamilyen 3rd party klaszter menedzsment technológia (pl.: Microsoft Windows Compute Cluster Server 2003, Microsoft Windows High Performance Computing Server 2008, Sun Grid Engine, stb.)
- Remote Kernels:
Távoli shellen keresztül történik a dolgozó kernelek indítása. Általában ennek a megoldásnak a konfigurációja és karbantartása a legkörülményesebb.
Beállítások és monitorozás
A párhuzamossággal kapcsolatos beállítások az Evaluation>Parallel Kernel Configuration... menüben érhetők el, ahol a különböző csatlakozási módokhoz érhetők el az alapértelmezett beállítások. A lokális kernelek esetén az alapértelmezett az, hogy a Mathematicát futtató gép magjaival egyenlő számú kernelt indít.Párhuzamos kiértékelés
Az egyik legelső parancs, amivel a párhuzamos rendszerünket ki tudjuk próbálni, az a ParallelEvaluate. Az argumentumaként megadott aktuális paramétereket kiértékeli mindegyik elérhető kernelen (vagy a paraméterként megadottakon: ParallelEvaluate[cmd, {kernels...}]), majd a kernelektől kapott eredményeket egy listában visszaadja. Amennyiben ez az első párhuzamos számítás, akkor a mester gép az előre bekonfigurált párhuzamos kerneleket elindítja. Hasznos lehet a Parallel Kernels Status ablak, ahol a futó kernelekről szerezhetünk információkat (terheltségük, általuk használt rendszer erőforrások).
In[2]:= ParallelEvaluate[$ProcessID]
Out[2]= {5704, 2636}
A ParallelEvaluate nem használható ha a - későbbiekben tárgyalt - ParallelSubmit vagy WaitAll parancs folyamatban van. Ha a kifejezésünkben nem csak beépített, hanem általunk definiált függvényeket vagy változókat is felhasználunk, akkor azokat előbb a DistributeDefinitions függvényt használva a többi kernelnek is el kell juttatni, vagy osztott memóriát kell használni, esetleg a With függvénnyel specifikálni kell a szimbólumok jelentését (ez lényegében a kifejezés definíciójának behelyettesítését hajtja csak végre).
In[19]:= mykernel = First[Kernels[]]
Out[19]= KernelObject[1, "local"]
In[20]:= a = 2; ParallelEvaluate[a === 2, mykernel]
Out[20]= False
In[21]:= With[{a = 2}, ParallelEvaluate[a === 2, mykernel]]
Out[21]= True
Kifejezéseink párhuzamos végrehajtódásához a ParallelCombine függvényt használhatjuk. A ParallelCombine[f,h[e1,e2,...,en],comb] utasítás kiértékeli az f[h[e1,e2,...,en]] függvényt szétosztva f[h[ei,ei+1,..., ei+k]] részekre a kernelek között, majd az eredményt a comb[] függvénnyel egyesíti. A comb alapértelmezetten h, ha h rendelkezik a Flat attribútummal (ez lényegében azt jelenti, hogy a művelet asszociatív), egyébként pedig a Join függvény.
Példák asszociatív függvény értékének kiszámítására:
In[26]:= ParallelCombine[Prime, {1, 2, 3, 4, 5, 6, 7, 8, 9}]
Out[26]= {2, 3, 5, 7, 11, 13, 17, 19, 23}
In[22]:= ParallelCombine[Identity, Unevaluated[1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9]]
Out[22]= 45
In[23]:= ParallelCombine[GCD, Unevaluated[GCD[4, 6, 8, 10]]]
Out[23]= 2
Mathematicában egy szekvenciálisan kiértékelt kifejezés végrehajtását automatikusan párhuzamossá tehetjük ha azt a Parallelize függvény paraméterének megadjuk.
In[19]:= mersenneQ[n_] := PrimeQ[2^n - 1]; DistributeDefinitions[mersenneQ]; Parallelize[Select[Range[1000], mersenneQ]]
Out[20]= {2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607}
Ezzel az utasítással sajnos nem minden kifejezés párhuzamosítható:
In[26]:= Parallelize[Integrate[1/(x - 1), x]]
During evaluation of In[26]:= Parallelize::nopar1:
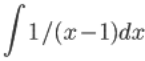 cannot be parallelized; proceeding with sequential evaluation. >>
Out[26]= Log[-1 + x]
cannot be parallelized; proceeding with sequential evaluation. >>
Out[26]= Log[-1 + x]
Párhuzamos folyamatok vezérlése
Mathematica-ban egy processz egy kiértékelendő kifejezés, egy processzor pedig egy párhuzamos kernel, mely a kiértékelést végrehajtja. Amennyiben több processz jön létre mint amennyi processzor van, akkor a fennmaradóak egy várakozási sorba kerülnek, és onnan kerülnek kiszolgálásra. A sorban lévő processzek mindegyike egy egyedi azonosítóval rendelkezik (evaluation ID, eid).A ParallelSubmit[cmd] utasítás egy kiértékelendő kifejezést rak a processzek várakozási sorába, és visszatér az utasítás eid -jével. A WaitAll[{eid1,eid2, ...}] utasítás várakozik a megadott processzek végrehajtására, és visszatér az eredményükkel. A WaitNext[{eid1 , eid2 , ...}] várakozik a megadott processzek valamelyikének befejeződéséig, és visszatér a {res, id, ids} hármassal, ahol id a befejeződott processz eid-je, res az eredménye, ids pedig a még kiértékelésre váró processzek eid-je. A WaitNext eredménye nem determinisztikus.
Rendelkezésre állnak alacsonyabb szintű műveletek is a Parallel`Developer` névtérben, melyekkel a várakozási sorhoz férhetünk hozzá és. A $Queue változó tartalmazza a kernelhez még hozzá nem rendelt processzeket, a $QueueLenght a sor hosszát. A ResetQueues[] megvárja a még futó processzek befejeződését, majd a eldobja a sorban lévő processzeket. A QueueRun[] összegyűjti a befejezett kiértékeléseket a kernelektől, majd újakat rendel hozzájuk a sorból. A visszatérési értéke igaz, ha legalább egy processzt hozzárendelt egy kernelhez vagy legalább egy eredményt kapott egy kerneltől. Alapesetben nincs szükség a QueueRun[] meghívására, csak ha saját magunknak implementáljuk a párhuzamos programunk fő ciklusát. Az eid -ekre a következő függvényeket tartalmazza a Parallel`Developer` névtér: ProcessID[pid] (visszatér az egyedi azonosítószámmal), Process[pid] (visszatér a kiértékelendő kifejezéssel), Scheduling[pid] (visszatér a processzhez tartozó prioritás-értékkel), ProcessState[pid] (visszatér a processz állapotával: befejezett, fut, várakozik). A WaitAll-t tekinthetjük bizonyos szempontból a ParallelSubmit inverzének is: a WaitAll[ParallelSubmit[expr]] az expr értékét adja vissza távoli kernelen kiértékelve, pont ahogy az expr kiértékelődne a helyi gépen is. A ParallelSubmit által generált pid-ek szimbolikus változók, melyeket nem szabad megváltoztatnunk, törölnünk vagy duplikálnunk a WaitAll lefutása előtt, mivel ezek mindegyike egy folyamatban lévő párhuzamos számítást reprezentál melynek értékét pontosan egyszer kell megkapni.
Ha pidek elvesztek vagy duplikálódtak, akkor az AbortKernels[] utasítást kell meghívnunk, mely a kerneleket új kiértékelés fogadására kész állapotba állítja. Amennyiben valamely kernel nem válaszol, az törlődik a Kernels[] által visszaadott kernelek listájából.
Távoli definíciók
A párhuzamos kerneleknek nincs hozzáférésük sem a master kernelen definiált változókhoz, sem pedig a lokálisan definiált függvényekhez. A Mathematica tartalmazza a már korábban említett DistributeDefinitions parancsot, mellyel könnyedén átadhatunk lokális definíciókat a párhuzamos kernelek számára. A legnagyobb előnye azonban az utasításnak az, hogy a használt package-eknek nem kell telepítve lenni a távoli kerneleken; a packagek tartalma a létrejött kapcsolaton keresztül adódhat át. Használatakor nem csak szimbólumokat adhatunk meg paraméternek, hanem egy teljes contextet is. Példa:
In[1]:= fl[n_] := Length[FactorInteger[2^n + 1]]
In[3]:= DistributeDefinitions[fl]
In[4]:= ParallelTable[fl[k], {k, 50, 60}]
Out[4]= {5, 5, 3, 3, 6, 5, 3, 4, 3, 4, 4}
Virtuális megosztott memória
A virtuális megosztott memória egy olyan programozási modell amely a szétosztott memóriát használó processzorokat lehetővé teszi úgy programozni, mintha azok egy közös, egymás között megosztott memóriaterületet használnának. A Mathematicában a párhuzamos feldolgozás feladatát egymástól független kernelek látják el. Ezek - még ha azonos gépen futnak is - különböző virtuális memóriaterületet használnak, azonban a Mathematica-ban lehetőség van a kernelek között megosztott virtuális memória használatára. A Mathematicában ez a modell a következőképpen működik: ha egy a változó megosztott, akkor bármely kernel, mely olvasni akarja, egy a master kernel által felügyelt, közös értéket olvas, íráskor pedig a megosztott érték fog változni, így a kernelek a következő olvasáskor már az új értéket olvassák. Az osztott változók használatának egy hátulütője hogy - mivel írása és olvasása hálózati műveleteket igényel, így - elérése lassabb a lokális változókénál.A SetSharedVariable[s1, s2, ...] parancs az si szimbólumokat megosztott változóként, a SetSharedFunction[f1, f2, ...] parancs pedig az fi szimbólumokat megosztott függvényként deklarálja. A megosztott változókat a $SharedVariables, a megosztott függvényeket a $SharedFunctions paranccsal érhetjük el. A szimbólumok megosztását az UnsetShared[s1, s2, ...] szüntethetjük meg, az UnsetShared[patt] paranccsal a patt mintára illeszkedő összes változó és függvény megosztását leállíthatjuk. A megosztott változók műküdése a következőképpen változik:
| s | a változó értékét a mester kerneltől kapja |
| s = e, s := e | az értékadés a mester kernelen hajtódik végre |
| s++, s--, ++s, --s, s += k, s -= k, s *= k, s /= k, AppendTo[s, k] | a műveletek a mester kernelen hajtódnak végre, és a felsorolt műveletek atomiak (ennek a szinkronizáláskor van szerepe) |
| Part[Unevaluated[s], i] | csak s egy részét küldi át a mester a MathLink kapcsolaton keresztül, nem pedig a teljes s-et |
| s[[i]] = e | s megadott részének új értéket ad |
In[1]:= ParallelEvaluate[$ProcessID]
Out[1]= {4928, 4340}
In[2]:= x = 17; SetSharedVariable[x]
In[4]:= r1 = Kernels[][[1]]; r2 = Kernels[][[2]];
In[5]:= ParallelEvaluate[x, r1]
Out[5]= 17
In[6]:= ParallelEvaluate[x = 18, r2]
Out[6]= 18
In[7]:= x
Out[7]= 18
In[8]:= ParallelEvaluate[x, r1]
Out[8]= 18
Szinkronizálás
Abban az esetben, amikor több, párhuzamosan futó kernel próbálja ugyanazt a megosztott változót írni és olvasni, akkor nem lehet garantálni, hogy egy olvasás és írás között valamely másik kernel nem módosította a változó értékét. Az kiolvasás és kiírás közti részt nevezzük kritikus szakasznak. Erre egy példa:
In[10]:= SetSharedVariable[y];
In[11]:= y = 0;
ParallelMap[(Pause[0.4 Random[]];
(*kritikus szakasz kezdete*)a = y;
Pause[Random[]];
y = a + 1
(*kritikus szakasz vége*)
) &, Range[10]]
Out[12]= {1, 2, 3, 2, 3, 4, 4, 5, 5, 6}
In[13]:= y
Out[13]= 6
Az y kimenő értékének 10-nek kellett volna lennie. A végrehajtás során amikor egy kernel a kritikus szakaszhoz ér, akkor a kritikus szakasz alatt más kernelnek nem szabadna az y változóhoz hozzáférni. A kritikus szakaszt lehet lock-kal védeni, hogy egyszerre csak egy kernel tudjon oda belépni. A CriticalSection[lck, expr] utasítás erre való: megszerzi a lockot, kiértékeli az utasítást, majd elengedi a lockot. Amint egy processz megszerzett egy lockot, azt más processz már nem kaphatja meg; addig kell várnia, míg azt a korábban meg nem szerző processz el nem engedi. A lock megszerzésére irányuló kísérletek között a processzek várnak mindig egy ideig, hogy a master kernelt ne terheljék túlságosan a kérésekkel.
Az előző példa, most már helyesen:
In[10]:= SetSharedVariable[y];
In[14]:= y = 0;
ParallelMap[(Pause[0.4 Random[]];
CriticalSection[{lck}, a = y;
Pause[Random[]];
y = a + 1;
a + 1]) &, Range[10]]
Out[15]= {1, 3, 5, 2, 4, 6, 7, 9, 8, 10}
In[16]:= y
Out[16]= 10
A lockolás lelassítja a számítást, mert a processzek várakozhatnak lockok feloldására. A fenti példában a végrehajtás lényegében szekvenciálisan történt. Kifejezések írásakor mindig törekedni kell a kritikus szakasz a lehető legrövidebbre való csökkentésére. Ha két processznek már vannak lockjai, és mind a kettő a másik lockjának a megszerzésével próbálkozik, akkor holtpont alakul ki, és a futásuk nem áll le.