
A modern technika, a korszerű termelési módszerek minden szinten elengedhetetlenné teszik a tervezést, és egyre követelőbben sürgetik a tervezés minél jobb megalapozottságát, amit a számítástechnikai és matematikai eszközök egyre szélesebb és mélyebb megismerése, és alkalmazása is elősegít. A tervezés lényeges mozzanata az ellenőrzés. Ennek azonban nemcsak a tervteljesítés ellenőrzésére, hanem annak a vizsgálatára is ki kell terjednie, hogy jó-e a terv. A szimuláció azon módszerek egyike, amely a kísérletezéshez hasonlóan gyorsan, és viszonylag olcsón ad eredményeket. A szimuláció a modelleken, a modellezésen alapul.
A rendszer és modellje
A rendszer - röviden megfogalmazva - elemek és a közöttük levő kapcsolatok összessége. Egy rendszerben az elemek lehetnek bármik (tárgyak, emberek, utasítások, jelek, információk, gépek, stb.), és kapcsolatuk is ezerféle lehet. A rendszert nemcsak elemei és az azok között levő kapcsolatok teszik rendszerré, hanem az is, hogy valahol meghúzzuk a rendszer határát, elkülönítjük környezetétől és ezáltal viszonylagosan izoláljuk. Az elkülönítés sohasem lehet teljes: a rendszer kívülről anyagot, energiát, információt, stb. kap (ezt nevezzük bemenetnek). Ez számára legtöbbször külső adottság. Ugyanakkor a rendszer kifelé, a környezete felé szintén továbbít anyagot, energiát, vagy információt (ezt nevezzük kimenetnek), ami viszont már a környezet számára jelent kész eredményt.
A rendszereket legtöbbször alrendszerekre lehet és célszerű bontani. Ezek a rendszer viszonylag önállóan működő részei, bár az alrendszerek egyszerű összesítése még nem adja ki magát a rendszert (pl. egy vállalat sem csupán osztályainak és műhelyeinek egyszerű együttese). Ez az alrendszerre bontás nagyobb rendszerek esetén szinte szükségszerű: az elemek és kapcsolatok elemzését első lépésben csak a különálló alrendszereken végezzük el, és csak azután keressük meg az alrendszerek közötti további kapcsolatokat, felépítve ezzel magát a rendszert (dekompozíció, analízis, szintézis).
A rendszerek többféleképpen osztályozhatók, de minket csak az egyik szempont érdekel közelebbről: az, hogy a rendszer determinisztikus-e, vagy sztochasztikus? Determinisztikus egy rendszer akkor, ha benne csak előre jól definiálható folyamatok zajlanak le, egyébként sztochasztikus.
A determinisztikus rendszerek legtöbbje jól algoritmizálható, így programozható is: modellezése egyszerű, az eljárás orientált programozási nyelvek használata itt kellő eredményt biztosít. A GPSS fő alkalmazási területe a sztochasztikus, véletlenszerű rendszerek, és ezek működése.
A modell a rendszer egy vetülete, lényegtelen tulajdonságoktól elvonatkoztatott mása. Magában foglalja a rendszer minden szempontból lényeges elemét és kapcsolatát. Működésében is a rendszert utánozza. A modell kialakításának folyamatát nevezzük modellezésnek. A modell célja általában nem önmagában rejlik, hanem a valódi rendszer tanulmányozása, vizsgálata a fő feladat. Tehát a modellnek működőképesnek kell lennie, mégpedig könnyen működtethetőnek, könnyen javíthatónak, és áttekinthetőnek. Emiatt a rendszeren kívül a rendszer bemeneteit, sőt néha a rendszert érő zavarásokat is modellezni szokták: azaz itt is általánosítanak, egyszerűsítenek.
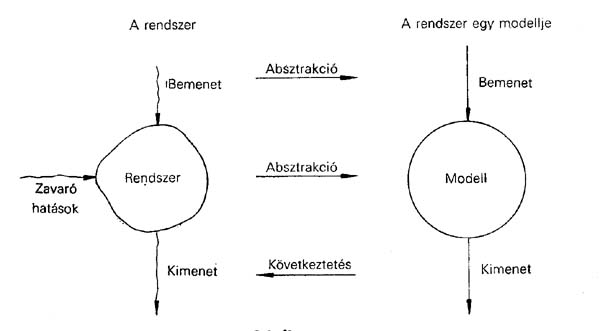
Az ábrán ezt a folyamatot mutatjuk be (stílszerűen szólva itt a modellezés modellje látható). A modell működtetésének eredménye a modell kimenete lesz. Ezt lehet azután a modellezés utolsó lépésében felhasználni arra, hogy az eredeti rendszer várható kimenetére, annak stabilitására vagy teljesítőképességére vonatkozólag információkat szerezzünk. Azt a folyamatot, amikor a rendszer vizsgálata céljából modellt építünk, majd azt működtetjük (vagyis a modellen kísérletezünk), szimulációnak nevezzük. Az elképzelés nem új: a primitív törzsi vadászok is modelleken, rajzokon gyakorolták a vadászat mozdulatait, a hadvezérek már az ókorban is kis bábukkal és terepasztalon tervezték meg a csatákat, és folytathatnánk még számtalan példával.
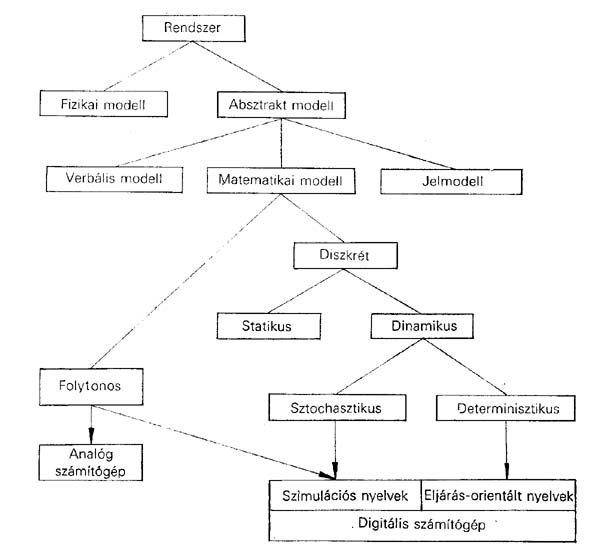
A modell lehet fizikai, absztrakt, vagy ezek kombinációja. A fizikai modell leggyakoribb formája a kicsinyítés (pl. a földgömb, vagy egy repülőgép modellje a szélcsatornában). Az absztrakt modell lehet verbális (pl. amikor elmesélik egy rendszer működését), matematikai (ekkor a rendszer leírása számokkal és egyenletekkel történik), és számítástechnikai (vagyis blokkdiagrammal vagy programmal írják le). A GPSS a blokkdiagramos modellezésre épül: a rendszer elemeit visszavezetjük néhány alaptípusra (ezeket nevezzük alkotóelemeknek), míg a közöttük levő, és időben változó kapcsolatokat mozgó elemekkel alakítjuk ki (ezek a tranzakciók) vagy logikailag kapcsolunk össze eseményeket. A kapcsolatok szerkezetét, a rendszer működésének folyamatait jól meghatározott lépésekre bontjuk (egy-egy ilyen lépést nevezünk blokknak). Mindez kellő egységbe ötvözve egy blokkdiagram-modellt ad, amelyet GPSS-ben programozva a modell működőképessé, időbeli változásokra is alkalmassá tehető.
A modell értéke
A szimuláció legfontosabb feladata a jóslás. Válaszolni arra a kérdésre: "Mi lenne akkor, ha...?" A szimuláció alapjául szolgáló modell jóságának fő kritériuma tehát az, hogy mennyire használhatók az eredmények? Természetesen van egy további szempont is: mi az ára, mik a feltételei a megbízható eredményeket nyújtó modell elkészítésének?
A modellezés nagy előnye, hogy nem állít korlátot a rendszer, vagy a modell bonyolultsága elé. Sőt, a rendszer és a modell komplexitásának sem kell feltétlenül kapcsolatban állniuk. A bonyolultság azonban veszélyes tényező: előfordulhat, hogy egy bonyolult rendszerről bonyolult modellt akarunk előállítani, és ettől a modellünk használhatatlan lesz, pedig apró egyszerűsítésekkel is kellő pontosságon belül maradhattunk volna. Más esetekben egy pici hanyagság azután továbbgyűrűzik, és az egész szimulációt tönkreteszi.
A modell másik, nagyon jól kihasználható tulajdonsága, hogy benne érzékelő pontokat, figyelő- és mérőváltozókat helyezhetünk el, így nemcsak a kimenetből kell következtetnünk a rendszer belső állapotaira, hanem közvetlen információk is rendelkezésünkre állnak. Ily módon a rendszer teljes jövőbeni élete, állapotainak halmaza felderíthető (természetesen a modell meghatározta egyszerűsítéseken belül).
A modellel kapcsolatban könnyen változtathatók a paraméterek. Ily módon tetszőleges számban és kombinációban deríthetők fel várható helyzetek. Két lehetőséget említünk meg: az időt, és a tiltott, vagy lehetetlen helyzeteket. Az időt úgy alakíthatjuk (felgyorsítjuk vagy lelassítjuk), ahogy nekünk megfelelő. Másrészt viszont a modell nemcsak a rendszer normális viselkedéseit tudja előre jelezni, hanem olyan eseteket is, amelyek szokatlanok, tönkretennék a rendszert, megvalósításuk túl drága, stb. (pl. ilyen a rendszer túlterhelése, háborús stratégiák tervezése, szervezési variációk hatása).
A modell előnyére szolgál, ha flexibilis. Gyakran nem az a célunk, hogy egy adott rendszerről ismereteket tudjunk meg, hanem az, hogy egy tervezett, vagy módosítani kívánt rendszer optimális változatát megtaláljuk. Ehhez a modellt nemcsak a való életből vett adatokkal, de mesterségesen előállított, tervezett, lehetségesnek tartott, vagy akár abszurd adatokkal is el tudjuk látni, hogy működését többféle körülmény között is tanulmányozni lehessen, miközben paramétereit változtatva azok legmegfelelőbb értékét keressük.
A szimuláció alapelve
A modellezés első lépése a vizsgálni kívánt rendszer meghatározása, a határvonal meghúzása: rendszerünket konkrétan el kell különítenünk - legalábbis gondolatban - a környezettől, meg kell határoznunk a bemeneteket, a lehetséges zavaró hatásokat, és tervezett rendszer esetén a kívánt kimenetet is.
Ezt követi - az egyszerűtől a bonyolult felé haladva - a rendszer megismerése. Ez az elemek és kapcsolatok feltérképezésével kezdődik, az ezekből kialakuló alrendszerek kialakításával folytatódik, és a teljes rendszer összeállításával fejeződik be. E folyamatba kell beépíteni a lényeges és elhanyagolható mozzanatok különválasztását, az elemek és kapcsolatok sematizálását, valamint az alrendszerek lehetőség szerinti önállósítását. Mindezt természetesen a bemenetre is el kell végeznünk.
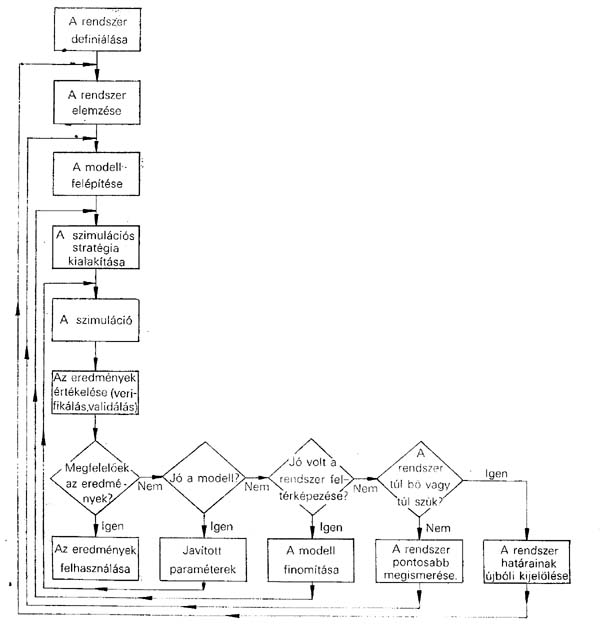
A következő lépés: az előbbi elemzés alapján a modell kialakítása, amit a szimuláció követ A szimuláció, és az azt követő kiértékelés iteratív folyamat. Ekkor zajlik tulajdonképpen az összes megelőző lépés ellenőrzése. Ez az eredmények valószínűsítésével, az elmélettel vagy gyakorlattal való összevetésével, a modell paramétereinek változtatgatásával, stb. történhet. A jó modell általában hosszú próbálkozások, tévedések útján alakul ki. Ebben a folyamatban nagy szerepe van a modellező felkészültségének és ötletességének. Más matematikai modellek (pl. a lineáris programozás) konkrét, egyértelmű, és megbízható optimumot adnak, ha létezik az optimum. Úgy tűnik, mintha a szimuláció kevésbé hatékony lenne ezeknél. Azonban ez nem így van: a kétféle módszer nem hasonlítható össze. A szimuláció kiváló módszer ott, ahol a többi hatástalan. Ez a módszer olyan területeken is alkalmazható ahol a matematikának még nincsenek eszközei.
További fontos, és egyáltalán nem elhanyagolható két lépés a szimulációs modell érvényességének megvizsgálása (validálás), és helyességének bebizonyítása (verifikálás). Az érvényesség ténye azt biztosítja, hogy a szimulációs modellből levezetett következtetéseink helyesek lesznek a valódi rendszerre való alkalmazáskor is. Lehetetlen, hogy bármely modell egy valódi rendszer reális, igaz képét adja. Sajnos a modell valódiságának bebizonyítása ritkán szerepel a modellezés egy lépéseként. Ahelyett, hogy ezt egy viszonylag független eljárással intéznénk el, gyakran a modell eredményeinek, egy-egy (talán éppen esetleges) eredményének egyezése csak az érvényesség kimondásának alapja. Ennek alapján szerencsétlen következtetések is születhetnek.
Az érvényesség "tesztelésére" valójában nincs egzakt módszer vagy eljárás. A modellezőnek egy háromlépéses vizsgálattal kell erről meggyőződnie. Elsőként meg kell bizonyosodnia, hogy a modell extrém szélsőséges esetekben is megmagyarázható eredményeket ad. Gondolunk itt arra hogy ha a modell túlterhelés vagy alulterhelés esetén átlagos, vagy éppen ellenkezőleg lehetetlen nem magyarázható eredményeket ad, akkor feltehető, hogy a modellünk csak egy konkrét esetre van jól "belőve", nem pedig az esetek többé-kevésbé széles skálájára.
Másodikként természetesen azt kell megvizsgálnunk, hogy a modell eredményei valószínűsíthetők-e. Harmadsorban pedig olyan embereket is be kell vonnunk a vizsgálatba, akik konkrétan is a rendszerben dolgoznak, és meg kell kérdezni őket, hogy a modell eredményei mennyiben egyeznek saját tapasztalataikkal. Természetes, hogy ha a fenti vizsgálatokat több különféle szempontból, több variánssal végezzük el, az érvényesség igazolása is teljesebb lesz. A modell érvényességének vizsgálata mellett értelemszerűen meg kell vizsgálni a rendszer bemeneteinek (így a feltételezéseinknek), valamint a kimenetnek az érvényességét is.
A helyesség igazolása azt a feladatot jelenti, hogy bebizonyítsuk, a modell pontosan azokkal a tulajdonságokkal rendelkezik, amikkel a modellező el akarta látni, de azokkal ténylegesen Ennek ellenőrzéséhez is csak a program ismételt átvizsgálása áll rendelkezésünkre, a korábbiakban már említett érzékenységi vizsgálatok formájában. Mindezek a tesztelési folyamatok gyakorlat problémákat is felvetnek: már kisméretű próbaadatok előállítása is költséges lehet; a próbaadatok sem méretben, sem összetételben nem tükrözik a tényleges bemeneteket; akár a bemenő, akár a kimenő adatok túl aggregáltak; kérdéses az adatok érvényessége; stb.
A szimuláció korlátai
A feladat megoldásához szimulációt ott alkalmazunk, ahol a más - analitikus vagy algoritmizálható - módszerek már nem segítenek. Konkrét analitikus módszereket a feladat minden. olyan részénél alkalmaznunk kell, ahol lehet, és csak a fennmaradó esetekben gondoljunk szimulációra. Tekintsük ezt egy általános korlátnak, amelyet néhány speciálisabb szempont is kiegészít. Ezeket nem árt szem előtt tartani a modellezés során, főleg az eredmények kiértékelésekor.
A szimuláció nem feltétlenül szolgáltat optimumot. Ez utóbbit csak több szimulációs lépé egymásutánjával érhetjük el, de közben nem számíthatunk biztos útjelzőkre, amelyek egyértelműen jeleznék a legrövidebb utat. Ez a feladat a jellemző tényezők kiválogatásával és értékelésével együtt a felhasználóra hárul.
A szimuláció eredményeinek pontossága sokszor előre nem megbecsülhető. Ennek fő oka a képletek vagy algoritmusok pontosságának hiánya, és a véletlenszerű jelenségek kiterjedt megjelenése. A pontosság növelhető a minél nagyobb számú szimulált eseménnyel, bár ez egyben növekvő gép időigénnyel, így emelkedő költségekkel jár.
A modell érvényességének, megbízhatóságának eldöntése rendkívül nehéz. A GPSS nagy számban ad hibajelzéseket, de ezek csak a program formáját és belső logikáját érintik közelebbről a rendszer és a modell, sőt a modell és a program közötti kapcsolat helyességét nem. A GPSS modell egyszerűsége, uniformizáltsága veszélyes és félrevezető lehet: vagy túl egyszerűnek tételezzük fel a valódi rendszert is, vagy pedig tökéletesen meg akarjuk valósítani a rendszert minden kis részletével együtt. Mindkét esetben az absztrakció mértékében van a hiba: túlbonyolítottuk, vagy leegyszerűsítettük a feladatot, így vagy pazarlók, vagy felelőtlenek voltunk. Bizonyos egészséges absztrakcióra mindig szükségünk van, de arra is gondoljunk, hogy következtetéseinket sohase terjesszük modellünk határain túlra!
A validálatlan modellek eredményeinek kiértékelésénél célszerű az eredményeket csak tendenciáknak tekinteni, nem pedig konkrét, megbízható értékeknek. Erre nemcsak a pontosság megbízhatatlansága késztet, de a rendszer finomságaitól történt - nem ellenőrzött - elvonatkoztatások és a szimulációs technika "szögletessége" is ez irányba hat. A szimulációs modell nem tud igen különböző eseményekhez rugalmasan alkalmazkodni: az alkalmazkodást vagy kihagytuk a modellből, vagy túlságosan mechanikus a modell (pl. a modellben nincsenek kivételek, amíg a valóságban ilyenek előfordulhatnak).
Szimulációs nyelvek
A szimulációnak nevezett tevékenységnek csak egy lépése a modell számítógépes programmá alakítása, majd ennek lefuttatása. Mégis, ez a lépés egyáltalában nem mondható egyszerűnek csak éppen jobban definiálhatónak, jobban determináltnak. A modell és a program közötti kapcsolatot a szimulációs célra orientált programozási nyelvek hozzák létre. A GPSS korántsem az egyetlen ilyen célú nyelv.
Az első szimulációs programokat eljárás orientált nyelveken (legtöbbször FORTRAN-ban) írták. Ez sok tekintetben kielégítő volt, de a modellezési technika fejlődésével egyszerűsítések, tipizálások, specializálódások váltak szükségessé. Az ezeket magukba építő fordítóprogramokat, pontosabban az ezeknek megfelelő programozási nyelveket nevezzük szimulációs nyelveknek.
A szimulációs nyelveket egymástól a szimulációk válfajai közül kiválasztott elsődleges cél, a lehetséges tipizálások végrehajtásának módja, és végül a bázisként kijelölt számítógép típusa szerint különböztetjük meg. E szakaszban csak néhányat tárgyalunk röviden, inkább csak a tájékozódás céljából.
- GPSS (1961). Általános jellegű digitális szimulációra tervezett, blokkorientált, önálló nyelv. Tipizálja a rendszerek főbb elemeit (pl. sorban állások, kiszolgálóhelyek, raktárak, stb.); ezen elemek jellemző értékeit automatikusan figyeli; blokkokat ad meg, amelyek igen előnyösen illeszthetők a modellek egyébként is blokkdiagramos szerkezetéhez; tranzakciókat használ a modell időbeni változásainak végigkövetésére; részletes standard kiíratást biztosít. Üzemel az IBM DOS és OS operációs rendszerekben, tehát az IBM/360 és 370, valamint ESzR és egyéb számítógépeken.
- DYNAMO (1959). Az ipari dinamika elvére épülő folytonos szimuláció önálló nyelve. Fő hangsúly a visszacsatolásos, dinamikus kölcsönhatásokon, aggregált folyamatokon van: a szimulálandó rendszert egyenletrendszer formájában írja le, amelyet a szimulált idő folyamán mindig újra és újra kiértékel, és erről táblázatokat közöl. Az IBM 7090- és 7094-es gépein áll rendelkezésre, ma már elavult.
- CSMP (1964). Ez a szimulációs nyelv a rendszerben párhuzamosan zajló folytonos folyamatok, és nem a diszkrét események elemzésére szolgál. A rendszer folyamatai között létező kapcsolatokat a felhasználó integro-differenciálegyenletek formájában adja meg. Ezeket a CSMP a kezdeti értékek alapján, a múló idő különböző időpontjaira megoldja, és az eredményekről grafikus, vagy táblázatos formában listát készít.
- SIMSCRIPT (1962). Eseményorientált, FORTRAN-ra támaszkodó digitális szimuláció. Két részből áll: a modell statikus leírásából és a dinamikusságot biztosító eseményekből. Ez utóbbiak endogének (belső jellegűek) vagy exogének (külső jellegűek) lehetnek, és a felhasználó rutinokban definiálja ezeket. Az IBM 7090, 360 és 370, a CDC, valamint a UNIVAC számítógépeken futtatható.
- SIMULA (1965). Folyamatorientált, általános célú szimulációs nyelv. Az ALGOL blokkfelépítésén alapulva szimulációs célú bővítésekkel rendelkezik. Középpontban a folyamat áll, amely az események bekövetkezésétől függően különböző állapotba kerülhet.
- SIMPL/1 (1972). Szintén folyamatorientált, de PL/1-re alapozott nyelv. Átvette a PL/1 koncepcióját, így a PL/1 egy supersetjének tekinthető. A PL/1 rutinok használata kombinálódik a folyamatok, rendszerelemek és listák használatával.
- SIAS (1971). A GPSS Siemens/4004 és 7000 számítógépekre írt változata.
- SIKOS (1973). Az IBM CSMP/360 Siemens-számítógépekre írt változata.
Megemlítjük még a folytonos szimulációs nyelvek közül az ANALOG, ill. a digitális szimuláció köréből a GASP, a CSL, a SIMPAC, és az OPS-3 nyelveket.