
A Maple képes más forrásnyelvű programoknak átadni a vezérlést (persze csak a lefordított object kódnak), majd onnan visszatérni és folytatni a program futását. Mindez persze paraméterek átadását is jelenti. Különösen igaz ez a C/C++ nyelven írt programokra.
Mint a programnyelvek általában, a Maple is rendelkezik belső HELP-pel, azaz segítséget tudunk kérni a szerkezettel, típusokkal, működéssel kapcsolatban. Tájékoztatást kaphatunk a használható függvényekről, továbbá saját rutinjaink számára a Maple-ben megszokott stílusú segítő információt csatolhatunk, ami a későbbi használatot könnyítheti meg.
Lehetőség van a Maple-ben alapfokú hibakezelésre is, ugyanis tartozik a rendszerhez trace, azaz nyomkövetés funkció, ami az utasítások lépésenkénti elvégzését támogatja. Ezáltal jobban meghatározható, hogy egy esetleges hiba esetén hol van a probléma.
Mivel a Maple matematikai programnyelvnek tekinthető, nagyon sokféle matematikai problémával meg tud birkózni. Ilyen problémák: approximációs feladatok, lineáris algebrai számítások, közönséges differenciálegyenletek megoldása. A matematikában ismert és jelentős problémák megoldására a Maple kiválóan használható. Természetesen lényeges lehet, hogy a kiszámított eredményt "láttassuk" is, azaz fontos az értékek grafikus megjelenítése. Ezt a Maple kétdimenziós és háromdimenziós grafikával támogatja, így lehetőség van a szemléletes ábrázolásra. Természetesen különböző színekkel is dolgozhat a rendszer.
Egyenletek, egyenlőtlenségek, egyenletrendszerek
Egyenletek
A matematikában gyakran van szükség egyenletek megoldására. A Maple erre a solve utasítást használja.
Tekintsünk egy másodfokú egyenletet:
Az egyenlet bal és jobb oldalát lekérdezhetjük az lhs() és rhs(), vagy az op() függvénnyel.
bal := x^2
> jobb := op(2,e1);
jobb := 5x-6
Megoldás:
mo := 2,3
A megoldás kifejezéssorozat (exprseq) típusú. Visszahelyettesítéssel ellenőrizhetjük, hogy x = 2 valóban megoldása-e e1-nek. Ezt a subs paranccsal tehetjük meg.
4 = 4
Ha egy egyenletben több ismeretlen van, akkor a solve() függvény paramétereként meg kell adni, hogy mely ismeretlenekre akarjuk megoldani az egyenletet.
> solve(e2,x);
1/2*b
Paraméteres egyenleteknél feltehető az a kérdés, hogy a paraméterek milyen értékeire ad az egyenlet azonosságot. Ezen probléma megoldására szolgál az identity() függvény.
> solve(identity(e3,x), {a,b});
{a = 1, b = 3/2}
A következő két példában azt láthatjuk, hogy a Maple harmad- és negyedfokú egyenleteket is képes megoldani. A megoldást a komplex számok körében keresi.
> solve(e4);
2, -4 + 3I*sqrt(3), -4 - 3I*sqrt(3)
> e5 := x^4 - 4*x^3 - 8*x + 32 = 0:
> solve(e5);
2, 4, -1 + I*sqrt(3), -1 - I*sqrt(3)
Galois munkássága óta tudjuk, hogy az ötöd- és annál magasabbfokú polinomegyenletekre nincs általános megoldóképlet. Lássuk, mit kezd a Maple egy ötödfokú egyenlettel!
> mo := solve(e6);
mo := RootOf(_Z^5 - 4_Z + 2)
A RootOf az argumentumában található egyváltozós polinom vagy polinomegyenlőség zérushelyeit, illetve gyökeit reprezentálja. A Maple a RootOf jelölést használja az algebrai számok ábrázolására.
Ha az e6 egyenlet közelítő valós megoldásait szeretnénk megkapni, akkor az fsolve() parancsot kell használnunk.
-1.518512153, .5084994847, 1.243596391
Az ötödfokú egyenletnek a komplex számok teste felett öt megoldása van. Ezeket mind megkaphatjuk az allvalues paranccsal.
-1.518512153, -.1167918612 - 1.438447695 I, -.1167918612 + 1.438447695 I, .5084994847, 1.243596391
Legyen most az egyenlet bal oldala egy racionális törtkifejezés!
> solve(e7,x);
RootOf(_Z^5 - 4_Z + 2)
> fsolve(e7,x);
-1.518512153
Elgondolkodtató, hogy az előbbi három közelítő valós megoldás helyett most csak egyet kaptunk, pedig e7 bal oldala biztosan nem egyszerűsíthető. Ennek az az oka, hogy az fsolve racionális törtfüggvények esetén csak egy közelítő gyököt számol ki, de ha harmadik paraméterként megadunk egy intervallumot, akkor ott is kiszámol egy gyököt, már ha van ott gyöke az egyenletnek.
Például:
.5084994847
A realroot könyvtári eljárás a paraméterként megadott egyváltozós, egész együtthatós polinom gyökeit izolálja.
> n := numer(lhs(e7));
n := x^5 - 4x + 2
> l := realroot(n);
l := [[0,1], [1,2], [-2,0]]
Az l listában megkaptuk a számláló gyökeit tartalmazó intervallumokat. Ezek után az fsolve segítségével kiszámolhatók a közelítő valós gyökök.
Az e8 egyenlet példáján azt láthatjuk, hogy a solve() leválasztja a racionális gyököket, az fsolve() pedig megadja a közelítő valós gyököket.
> solve(e8);
-1/3, -1, RootOf(_Z^4 + 7_Z + 2)
> fsolve(e8);
-1.806225190, -1.000000000, -.3333333333, -.2866791954
Vegyünk most egy transzcendens egyenletet, és próbáljuk meg az fsolve-val megkeresni a közelítő megoldásokat.
> fsolve(e9,x);
2.792247796
Egy megoldást kaptunk, pedig nyilvánvaló, hogy több van. Most a realroot sem segít.
ERROR, (in realroot) first argument must be a univariate polynomial
Maradt még egy lehetőségünk. ábrázoljuk a 3sin(x) - ln(x) függvényt, és a grafikonról olvassunk le olyan intervallumokat, amelyekben a függvénynek zérushelye van, majd az fsolve segítségével határozzuk meg ezek közelítő értékét.
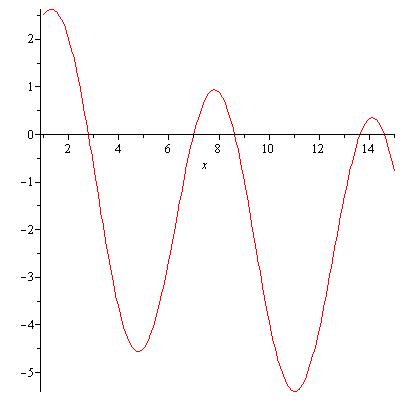
Most megkereshetjük az egyenlet [6,8] intervallumba eső gyökét. (Majd persze a továbbiakat is.)
6,988241068
Az, hogy az fsolve opcióként elfogad egy intervallumot, ahol a gyököt keresi, máskor is hasznos lehet. Például ha a feladat jellegéből adódóan több megoldással rendelkező egyenlet esetén csak bizonyos, mondjuk 2-nél nagyobb gyökökre vagyunk kíváncsiak. Ha ilyenkor a solve parancsot használnánk, akkor az összes megoldásból utólag le kellene válogatni a nekünk megfelelőket.
Néhány szó a trigonometrikus egyenletek megoldásáról:
Oldjuk meg a sin(x) = 0 és a sin(x) = cos(x) - 1 egyenleteket!
> solve(e10,x);
0
> e11 := sin(x) = cos(x) - 1:
> solve(e11,x);
-1/2*Pi, 0
A solve utasításra mindkét egyenlet alapmegoldását adta a Maple. Ha az összes megoldást meg akarjuk kapni, akkor a következő beállítást kell tenni:
> r := solve(e10,x);
r := Pi * _Z1~
A ~ jel azt jelenti, hogy a _Z1 paraméterre megszorítás érvényes, nevezetesen most csak egész szám lehet. A paraméternek értéket is adhatunk, például 3-at:
3*Pi
Egyenlőtlenségek
Egyenlőtlenségeket az egyenletekhez hasonlóan kell megoldani. Ilyenkor a megoldások nyílt vagy zárt intervallumok.
> solve(egyenlotl1);
RealRange(Open(-2),Open(1/2))
> egyenlotl2 := x^2 + 6*x - 27 >= 0:
> solve(egyenlotl2);
RealRange(-infinity,-9), RealRange(3,infinity)
Egyenletrendszerek
Egyenletrendszereket úgy tudunk megoldani, hogy a solve utasítás paramétereiként halmazban felsoroljuk az egyenleteket és a változókat.
> e2 := 5*x + y - 4*z = 0:
> e3 := 2*x - 3*y + z = 0:
> mo := solve({e1,e2,e3}, {x,y,z});
mo := {x = 11, z = 17, y = 13}
> x;
x
A példából láthatjuk, hogy a solve csak előállította a megoldáshalmazt, de az x változó nem vette fel a megoldás értékét. Ezért alkalmaznunk kell az assign eljárást, melynek paraméterként megadhatjuk a solve outputját.
> x,y,z;
11, 13, 17
A következő egyenletrendszernek végtelen sok megoldása van.
> e2 := x + 2*y + z = 0:
> e3 := -x - 1.5*y + 0.5*z = -6:
> mo := solve({e1,e2,e3}, {x,y,z});
mo := {z = z, x = 5. z + 24., y = -3. z -12.}
Az x^2 + y^2 = 25, x^2 + y^2 = 49 egyenletrendszernek nyilvánvalóan nincs megoldása. Mit szól hozzá a Maple?
> solve({x^2 + y^2 = 25, x^2 + y^2 = 49}, {x,y});
Semmit! Ugyanis általában ha a Maple egy feladatra a saját rendszerében nem talál megoldást, akkor egyáltalán nem jelzi azt, csak visszaadja a promptot. Itt nem arról van szó, hogy helytelenül adtunk meg egy parancsot. Olyankor figyelmeztető vagy hibaüzenet a válasz!
Grafika
Beszéljünk picit részletesebben a Maple grafikus képességeiről.
A Maple program grafikus eljárásait a plots csomag tartalmazza.
A síkbeli rajzolásra a plot parancs szolgál. Általános szintaxisa: plot(f,h,v), ahol:
f – az ábrázolandó függvény
h – vízszintes ábrázolási tartomány
v – függőleges ábrázolási tartomány
Pl.: rajzoljuk ki a szinuszfüggvényt a [-2Pi,2Pi] intervallumon:
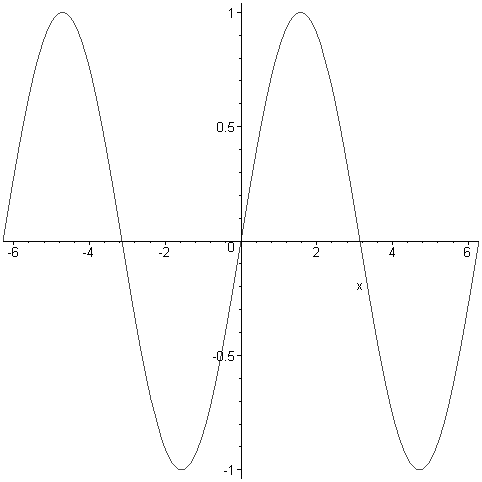
Jól látható, hogy csak a vízszintes tartományt adtuk meg, a Maple automatikusan állította be a függőleges tartományt a [-1,1] intervallumra.
Azonban, ha mi szeretnénk azt beállítani:
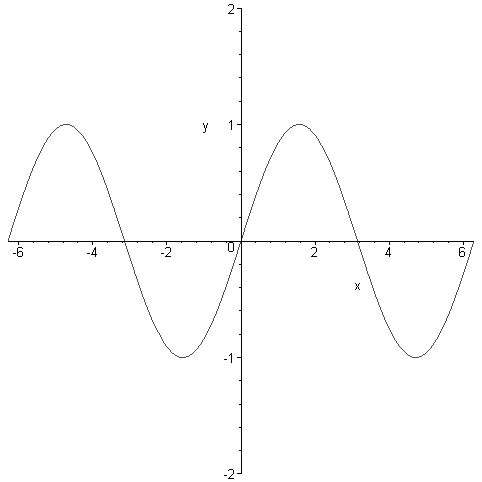
A plot parancsnak megadhatók különböző opciók is:
AXES: a koordinátatengelyek elhelyezkedésére utal
| AXES lehetséges értékei | Megjegyzés |
|---|---|
| BOXED | egy síknegyedben ábrázolja a függvényt a megadott vízszintes és függőleges tartomány szerint |
| FRAME | nem rajzol keretet |
| NONE | nem rajzolja be a tengelyeket |
| NORMAL | ez az alapbeállítás |
COLOR: paramétere a szín, az adott szín neve angolul
FONT: A szövegobjektumok jellemzőinek beállítására szolgál
Paraméterei:
- típus: times, courier, helvetica, symbol
- stílus: roman, bold, italic, bolditalic
- méret: egész szám, pontokban megadva
Paraméterei: [x, y]
x: az x tengely felirata
y: az y tengely felirata
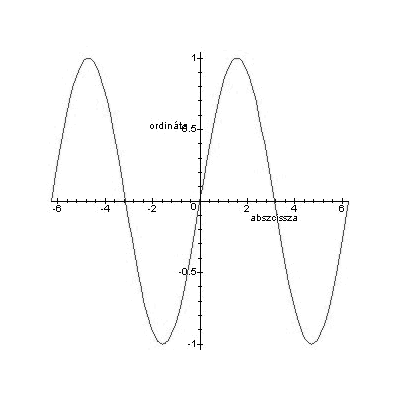
TITLE, TITLEFONT: Az ábra címe, illetve a cím szövegének jellemzői
AXESFONT: A koordinátatengelyek szövegobjektumainak jellemzői
XTICKMARKS, YTICKMARKS: Megadhatjuk vele a tengelyek minimálisan jelölt pontjainak számát, illetve a pontok feliratozását.
Paraméterei: ha n egész szám, akkor a pontok számát adhatjuk meg; ha lista, akkor a pontok feliratozását.
LINESTYLE: A vonal stílusát határozhatjuk meg.
Paraméter: n egész szám (n = 0..4)
NUMPOINTS: Mintapontok száma. Ha nem adjuk meg, akkor a Maple a következőképpen rajzol: kirajzolja a mintapontokat, majd összeköti őket egyenes szakaszokkal. Ha a görbe simasága úgy kívánja, felvesz egyéb pontokat is.
Paraméter: a mintapontok száma
SCALING: Tengelyek skálázásának megadása
Paraméter: constrained / unconstrained (arányos / nem arányos)
STYLE: Görbe rajzolásának stílusa
Paraméter: line (vonal), point (pont), patch (poligonok pontjainak összekötése), patchnogrid (mint az előző, a négyzetrács kirajzolása nélkül)
SYMBOL: Pontok rajzolásának stílusa
Paraméter: box (négyzet), circle (kör), point (pont), diamond (rombusz), cross (kereszt)
THICKNESS: Vonalvastagság beállítása
Paraméter: n egész szám (n = 1..5)
VIEW: A görbe egy részletének kiragadása
Paraméter: [x koordináta intervalluma, y koordináta intervalluma]
Azonban a Maple-ben lehetőség van 3D-s megjelenítésre is. Erre a plot3D parancs szolgál.
A parancs lehetséges formái:
plot3d([f, g, h], a..b, c..d)
Ahol:
| expr | x-et és y-t tartalmazó kifejezés |
| f, g, h | eljárások vagy operátorok |
| exprf, exprg, exprh | s-et és t-t tartalmazó kifejezések |
| a, b | valós konstansok, eljárások vagy y-t tartalmazó kifejezések |
| c, d | valós konstansok, eljárások vagy x-et tartalmazó kifejezések |
| x, y, s, t | nevek |
Szintén lehetőség van mindenféle beállításra: megadhatunk más típusú koordináta-rendszereket (alapértelmezett a Descartes-féle), a tartományhatárok függhetnek változóktól, változtathatunk a színeken stb.
Ezekről bővebb információt a Maple program helpjében lehet találni.
Újabb verziók
Ezen leírás alapját a Maple V verziója adta. Azonban az idő halad a maga útján, így ennek a programnak is újabb és újabb verziói jelentek meg. Az éppen aktuális a Maple 14.
Csak néhány új dolog, ami megjelent az újabb verziókban (a teljesség igénye nélkül):
- új matematikai Logika csomag (Maple 9.5-ben)
- a SolveTools csomag kibővített változata (Maple 9.5-ben)
- kibővített egyszerűsítések (Maple 9.5-ben)
- korszerűsített összegzés (Maple 9.5-ben)
- differenciálegyenlet rutinok a precíz ODE-hez (Maple 9.5-ben)
- többmagos rendszerekben támogatást nyújt a többszálú programozáshoz (Maple 11-ben)
- lehetőség van a listák adott hosszúságú allistákra történő darabolására (Maple 11-ben)
- mutexeket használ az adatstruktúrák ellenőrzésére (Maple 11-ben)
- új csomagok (Maple 11-ben):
Graph Theory (több mint 150 függvényt és több mint 35 előredefiniált grafikont tartalmaz);
Physics (matematikai fizika tárgyú csomag);
Differential Geometry (támogatja a számításokat a következő területeken: tenzorelemzés, Lie-algebrák, Lie-csoportok, transzformációcsoportok) - 3D plot kiegészítése új funkciókkal (tetszőlegesen bejárható 3 dimenziós grafikonok) (Maple 13-ban)