
Az alábbi program az X vektorban tárolt szavakat rendezi szóhossz alapján sorba. X[X+.¬' ';]
Egy program, amely 1-től N-ig megkeresi az összes prím számot:
(~N ą N°.×N)/N „ 1‡ ĽN
A következőképpen kell olvasni jobbról-balra:
- Ľ N egy vektort kreál 1..N-ig (ha N=6 a program kezdetekor akkor a vektor {1,2,3,4,5,6})
- Eldobjuk a vektor első elemét a ‡ függvénnyel, azaz az 1-et. Vagyis 1‡ ĽN az {2,3,4,5,6}
- N-et egyenlővé tesszük a kapott vektorral ( „ , megfeleltetés operátor)
- Descartes szorzatot készítünk NxN-nel, vagyis egy mátrixot, amelyben N minden elemét szorozzuk N miden elemével °.× függvény)
- Egy N hosszú vektort hozunk létre, 1-et állítva a miden pozíciójára, ahol N értéke szerepel a mátrixban ( ą tartalmazó függvény), vagyis {0,0,1,0,1}
- Logikailag negáljuk a kapott vektor értékét ( ~ negálás függvény), azaz {1,1,0,1,0}
- Kiválogatjuk azon elemeket N-ből, ahol a megfelelő érték 1 ( / függvény) vagyis {2,3,5}
Csomópontok végrehajtási ideje
Legyen egy Petri hálónk (irányított gráf, ahol a csomópontok valamilyen tevékenységek) Minden tevékenység csak akkor indulhat, ha a rá mutató nyilak csomópontjai már befejeződtek. A következő ábra egy ilyen hálót mutat, és annak reprezentációs mátrixát:
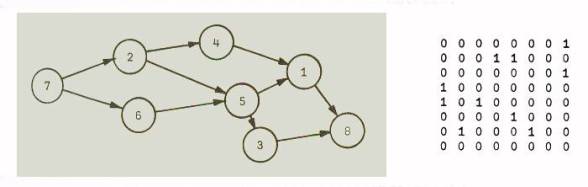
A mátrix ( MP[i;j] ) i. sorában ha a j. elemnél 1 van, akkor az i. csomópontba megy él a j-ből. Nyilvánvaló, hogy ennek a gráfnak körmentesnek kell lennie.
Van továbbá egy D vektorunk amiben a csomópontok időtartamát tároljuk.
A feladat: meghatározni, hogy mikor fog egy csomópont legkorábban elindulni és mikor fog legkésőbb befejeződni. Íme az APL forráskód, amit 1967-ben ennek a problémának a megoldására írt Montalbano:

Zsákjáték
Roger Hui által kitalált játék a következő: minden körben 12 kártyát osztunk a 81-es pakliból, amiből minden kártya különböző.
Minden kártya a következő jegyeket hordozhatja magában:
szám: 1, 2, or 3
alak: gyémánt, ovális, kacskaringó
szín: vörös, zöld, lila
minta: szolid, vázlatos, homályos
Egy “zsák” 3 kártyából áll, amelyeknek egyes jellemzői vagy ugyanazok, vagy különbözőek, pl:
2-es vörös szolid gyémánt
2-es vörös vázlatos kacskaringó
2-es vörös homályos ovális
A feladat: osztani 12 lapot és minden lehetséges zsákot felkutatni.
A megoldó program (ezt csak az APL tömörsége miatt hoztam fel, nem szükségszerű első látásra megérteni):
’ Z„DEAL;M;R
[1] ©Deals 12 cards
[2] R„(12?81)-1
[3] M„ł3 3 3 3‚R
[2] Z„M°.=0 1 2
’
’ Z„SETS H;F
[1] ©Returns all the sets in hand H
[2] F„H[3 COMBIN 12;;]
[3] Z„(^/^/2¬+/[2]F)šF
’
’ Z„FMT A;C
[1] ©Formats cards for display
[2] C„'1' '2' '3' 'Red' 'Green' 'Purple' 'Diamond' 'Oval' 'Squiggle' 'Filled' 'Hollow' 'Lined'
[3] Z„(Ż1‡˝A)˝(,A)/,(˝A)˝C
’
’ Z„HAND D;L
[1] ©Translates hand codes to the corresponding bit array
[2] D„MATRIFY D
[3] L„4 3˝'123RGPDOSFHL'
[4] Z„2 3 1łź/L°.=D
’
’ Z„X COMBIN Y;C;J;K;N
[1] ©Returns all possible combinations of ¸ items drawn from Ľľ
[2] © The result is origin-sensitive
[3] N„1+Y-X
[4] K„÷N © give domain error if X=Y+1
[5] K„(X-1)+ĽN
[6] Z„(N,×X)˝K
[7] R„N˝1
[8] L1:…(ŚIO>1†K„K-1)/0
[9] C„˛R„+\R
[10] J„(Ľ˝J)-J„C/+\0,1‡C
[11] Z„(C/K),Z[J;]
[12] …L1
’
’ Z„A MATRIFY V;D;L;I;W;M
[1] ©Forms a matrix from a vector or matrix of names ľ
[2] © The optional left argument is a vector of delimiter characters (which
[3] © separate the words in the right argument)
[4] © Treats multiple consecutive delimiters as a single delimiter
[5] ©
[6] …(1<˝˝Z„V)/0 © return argument unchanged if it's already a matrix
[7] –(0=ŚNC 'A')/'A„'' ''' © set left arg if user didn't supply one
[8] D„VąA © mark delimiters in V
[9] L„Ż1‡1,D © push a 1 into the front of each group of 0's
[10] V„(I„~D)/V © delete delimiters
[11] L„I/L
[12] I„L/Ľ˝L © find position of the first of each name
[13] W„(1‡I,1+˝L)-I © get the width of each name
[14] M„0——/W © width of the widest name
[15] V„(,W°.‰ĽM)\V © insert blanks at the end of short names
[16] Z„((˝W),M)˝V © convert to a matrix
’